Задача линейного программирования. Проверка оптимальности текущего плана, страница 15

1. Построить прямые, уравнения, которых получаются в результате замены в ограничениях (2) знаков неравенств на знаки равенств

.                     (3)

2. Найти полуплоскости, определяемые каждым из ограничений задачи.

3. Определить многоугольную область допустимых решений.

4. Если область решений является пустым множеством, то задача не имеет решения в виду несовместимости системы ограничений.

5. Если область решений является непустым множество, построить нормаль линий уровня  и одну из линий уровня, имеющую общие точки с этой областью.

6. Линию уровня переместить до опорной прямой в задаче на максимум в направлении нормали, в задаче на минимум – в противоположном направлении.

7. Если при перемещении линии уровня по область решений в направлении, соответствующем приближению к экстремуму целевой функции, линия уровня уходит в бесконечность, то задача не имеет решения в виду неограниченности целевой функции.

8. Если задача линейного программирования имеет оптимальное решение, то для его нахождения решить совместно уравнения прямых, ограничивающих область допустимых решений и имеющих общие точки с соответствующей опорной прямой.

9.Если целевая функция задачи достигает экстремума в двух угловых точках, то задача имеет бесконечное множество решений. Оптимальным решением является любая выпуклая линейная комбинация этих точек. После нахождения оптимальных решений вычислить значение целевой функции на этих решениях.

2.1.2.Единственность оптимального решения .Задача имеет единственное оптимальное решение, когда прямая Z и область решения в крайнем положении будут иметь одну общую точку.

Пример 1. Найти графически оптимальное решение системы неравенств

                                                                              (1)

                                                                             (2)

                                                                              (3)

                                                                            (4)

                                                                              (5)

                                                                              (6)

и минимизирующее максимизирующее и функцию Z=х₁+х₂.

Решение. 1. Строим прямую x₁-2x₂ = -12 (L₁), соответствующую ограничению (1). Полагая в уравнении x₁=0, получим 0-2x₂ = -12, т.е. x₂ = 6. Следовательно, прямая пересекается с осью ординат в точке (0, 6). Полагая в уравнении x₂=0, получим x₁-2∙0 = -12, т.е. x₁ = -12.

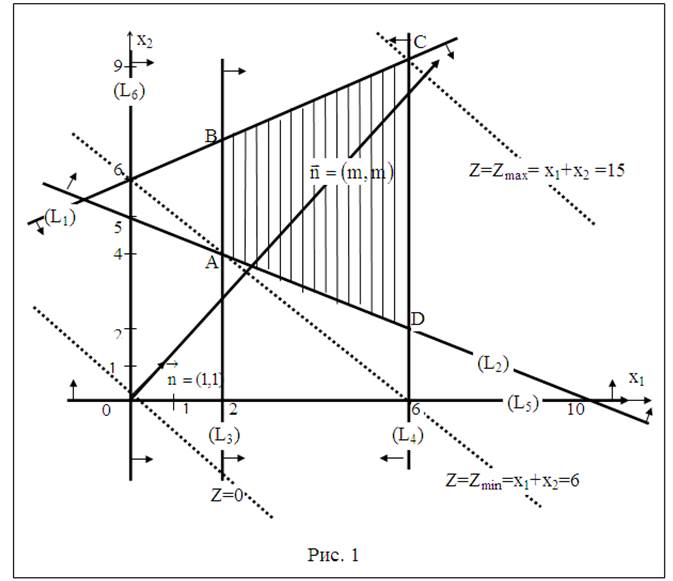
Это означает, что прямая пересекается с осью абсцисс в точке (-12, 0). Проводим прямую через точки (0, 6) и(-12, 0) (см. рис. 1).

2. Находим, какая из двух полуплоскостей, на которые эта прямая делит всю координатную плоскость, является областью решений неравенства (1). Для этого достаточно, координаты какой-либо точки, не лежащей на прямой, подставить в неравенство.

Так как прямая (L₁) не проходит через начало координат, подставляем координаты точки О (х₁=0, х₂=0) в первое ограничение 1·0-2∙0 ≥ -12. Получаем строгое неравенство 0>-12. Следовательно точка О(0, 0) лежит в полуплоскости решений. Таким образом, стрелки на концах прямой (L₁) должны быть направлены в полуплоскость, содержащую точку О(0, 0).

3.Аналогично строим прямые:

           (L₂),

                       (L₃),

                       (L₄),

                       (L₅),

                       (L₆)

и области ограничений (2)…(6).

4.Находим общую часть полуплоскостей решений. Областью решений является четырехугольник ABCD (см. рис. 1).

5.Построим нормаль линий уровня  и одну из этих линий, например х₁ + х₂ = 0, проходящую через начало координат О (0,0) и перпендикулярную – вектор .

6. Перемещаем линию уровня параллельно самой себе в направлении нормали . Прямая Z встретит четырехугольник решений в первой точке А.

7.Определяем координаты точки А=(L₂)Ç(L₁). Решая систему

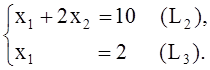   получаем.