Задача линейного программирования. Проверка оптимальности текущего плана, страница 17

                                                                                             (5)

Решение.1. Строим  область решений задачи. Для этого заменяем знаки неравенств в уравнениях ограничений на равенства:

                  (L₁),

                                (L₂),

                          (L₃),

                          (L₄),

                          (L₅).

Построив полученные прямые, найдем соответствующие полуплоскости и их пересечение.

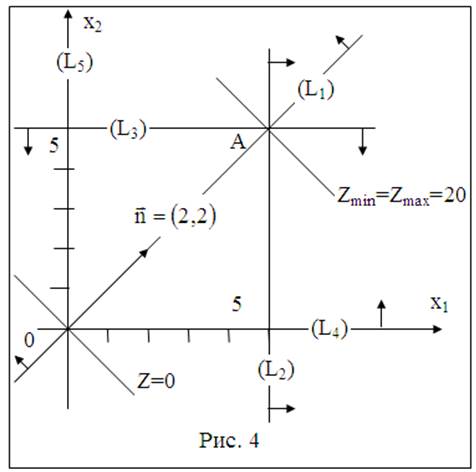
Как видно из рис. 4, областью решений задачи является единственная точка А=(5, 5).

2. Строим  прямую Z= 2x₁+2x₂ и вектор . Передвигая данную прямую в направлении вектора видим, что она проходит через точку А=(5,5). Следовательно, в этой точке функция Z принимает минимальное и максимальное значение, т.е. Z(А)=Z_min= Z_mах=2∙5+2∙5=20.

2.1.3. Бесконечное множество оптимальных решений

В этом случае в крайнем положении прямая Z проходит через грань области.

Пример 5. Найти максимум и минимум функции Z=8x₁+4x₂  при условиях:

                                                                                  (1)

                                                                                  (2)

                                                                                (3)

                                                                                             (4)

,                                                                                     (5)

                                                                                             (6)

                                                                                             (7)

Решение.1.Строим прямую 4х₁-х₂=0 (L₁), соответствующую ограничении (1). Полагая х₁=0, получим 4∙0-х₂=0 Þ х₂=0. Следовательно, прямая (L₁) пересекается с осью ординат в точке (0, 0). Полагая х₁=2 (число 2 выбрано произвольно), получим 4∙2-х₂=0 Þ х₂=8. Это значит, что прямая проходит через точку (2, 8). Проводим прямую через две найденные точки.

2.Определяем, какая их двух плоскостей, на которые эта прямая делит всю координатную плоскость, является областью решений неравенства(1). Для этого достаточно координаты какой-либо точки, не лежащей на прямой, подставить в неравенство. Так как прямая (L₁) не проходит через точку (0, 2), то ее координаты подставляем в ограничение (1), т.е. 4∙0-2≥0. Неравенство – не верно, следовательно, выбранная точка не лежит в плоскости решений. Таким образом, стрелки на концах прямой (L₁) должны быть направлены в полуплоскость, не содержащую точку (0, 2).

3.Аналогично строим прямые:

                (L₂),

             (L₃),

                          (L₄),

                  (L₅),

                          (L₆),       

                          (L₇)

и области решений для ограничений (2)…(7).

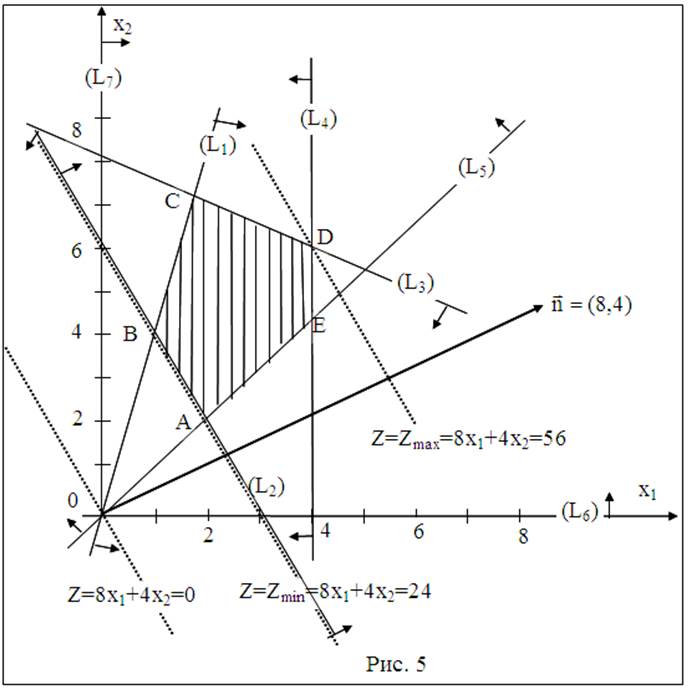
4.Находим общую часть полуплоскостей решений. Полученный пятиугольник ABCDE, является областью решений (см. рис. 5).

5.Строим вектор .

6.Строим прямую 8х₁+4х₂ =0 проходящую через начало координат

О(0, 0) и перпендикулярную вектору .

7. Перемещаем данную прямую в направлении вектора . Прямая Z встретит пятиугольник решений в отрезке АВ (прямая Z совпадает с граничной прямой (L₂) области допустимых решений и проходит через две угловые точки этой области А и В).

8.Определяем координаты точек А=(L₂)Ç(L₅) и В=(L₁)Ç(L₂), решая системы уравнений:

                     

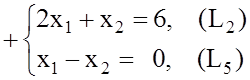
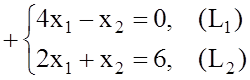
3х1=6;

6х1=6;

                                        

А=(2, 2);                                                      В=(1, 4).

9. Вычисляем Z(А)= Z(В)= Z_min = 8∙2+4∙2 = 8·1 + 4·4 = 24.

Согласно рис. 5 задача имеет бесконечное множество оптимальных решений, являющихся точками отрезка [A, В].  Таким образом, min Z(X) = 24 при

Общая формула для определения любого оптимального решения задачи (общее решение)

Х^* = (1-t)(2,2) + t(1,4) = (2-2t,2-2t) + (t,4t) = (2-t,2+2t),   0 ≤ t ≤ 1.