Задача линейного программирования. Проверка оптимальности текущего плана, страница 9

№	Б	Сб	В	-1	-1	0	0
				A1	A2	A3	A4
1	A3	0	1	-1	1	1	0	+
2	A4	0	2	1	-2	0	1	(1)  (1)
3			0	1	1	0	0

Находим оценки небазисных столбцов А₁ и А₂.

∆₁ = С_б ∙ А₁ – с₁ = (0, 0) ∙ (-1, 1) – (-1) = 1 > 0 , ∆₂ = С_б ∙ А₂ – с₂ = (0, 0) ∙ (1, -2) – (-1) = 1 > 0 .

Так как ∆₁ = 1 > 0, ∆₂ = 1 > 0, то Х₀ не оптимален. Произведем необходимые вычисления

θ₁ = 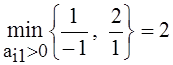  , V₁ = 1 ∙ 2 = 2 , θ₂ =  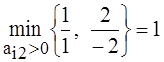 , V₂ = 1 ∙ 1 = 1 .

Так как V₁ > V₂, то выгоднее включить в базис столбец А₁. При этом ведущий элемент будет а₂₁ = 1.

2) Заполним вторую таблицу.

Так как ∆₂ = 3 > 0 , то Х₁ = (х₁=2, х₂=0, х₃=3, х₄=0) не оптимален.

Находим θ₂ = 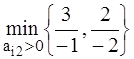 . В столбце А₂ нет положительных элементов, т.е. коэффициент при неизвестном х₂ в каждом из уравнений отрицателен. Поэтому оптимального решения не существует. Задача не имеет конечного оптимума min Z(X) = -∞.

Пример 9. Z(X) = x₁ – x₂ → max,

0x₁ – x₂ + x₃ + x₄ = 3,

x₁ – 2x₂ + 0x₃ + x₄ = 2,

x_i ≥ 0, i = 1,2,3,4.

Решение. Заполним первую симплекс-таблицу.

Так как ∆₂ = -1 < 0, то Х₀ = (х₁ = 2, х₂ = 0, х₃ = 3, х₄ = 0) не оптимален.

Находим  θ₂ = 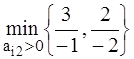. В столбе А₂ нет положительных элементов, т.е. коэффициент при неизвестном х₂ в каждом из уравнений отрицателен. Поэтому оптимального решения не существует. Задача не имеет конечного оптимума max Z(X) = +∞.

1.2.8. Метод искусственного базиса. Данный метод применяется для решения задачи ЛП симплексным методом в случае, когда задача не имеет первоначального решения с базисом из единичных векторов.

Пример 10.  Z (Х) = 7х₁ – 13х₂ – 8х₃ + 10х₄             min,               (1)

(2)

 х₁ – х₂ – 3х₃ +2х₄ = 3, х₁ –2х₂ –  х₃ +  х₄ = 2                                                                            х₁ –2х₂ –  х₃ +  х₄ = 2,                                                                           

x_i ≥ 0, i = 1, 2, 3, 4.                                                                          (3)

Решение.1)В левой части ограничений(2)вводим неотрицательные искусственные переменные  х₅, х₆.

2) Данная задача – задача на нахождение минимума, поэтому х₅ и х₆ в целевую функцию вводятся с коэффициентом  +М. Получаем

Z (Х) = 7х₁ – 13х₂ – 8х₃ + 10х₄ + Мх₅ + Мх₆ → min,                      (4)

(5)

 х₁ – х₂ – 3х₃ +2х₄ + х₅ + 0х₆ = 3,                                                    х₁ –2х₂ –  х₃ +  х₄ + 0х₅ + х₆ = 2,