Задача линейного программирования. Проверка оптимальности текущего плана, страница 6

20) Так как ∆_j ≥ 0 при j=1,2,3,4,5,значит текущий план Х^*=Х₁=(2, 0, 6, 0, 1) оптимален, а максимальное значение функции Z(X) равно max Z(X) =Z(X₁) = 4.

21) Проверка:  2 + 0 + 0(6) – 6(0) – 1 = 1 ,0(2) + 0 + 0(6) + 0 + 1(1) = 1 ,0(2)+0+ 6–3(0)–4(1) = 2 , х₁ = 2 > 0 ,  x₂ = 0 ,  x₃ = 6 > 0 ,  x₄ = 0 ,  x₅ = 1 > 0.

Z(X) = - 1(2) + 0 + 6 = 4.

2°) Если столбцов A_j с положительными (отрицательными) оценками ∆_j > 0 (∆_j < 0) несколько, то находим сначала θ_j для каждого столбца с положительной (отрицательной) оценкой по формуле θ_j =      =    ,  , . . . ,    .

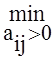
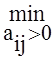
Выгода V_j находится по формуле V_j = ∆_j∙θ_j.

Включить в базис тот столбец A_j, для которого выгода V_j максимальна. При этом ведущим элементом окажется тот элемент, а′_ij, при котором получено число θ_j, то есть тот элемент,  а′_ij, для которого отношение  - самое малое при переборе всех строк таблицы с а′_ij>0.

1.2.5. Единственность оптимального плана. В задаче на минимум  или на максимум, оптимальное решение является единственным, если ∆_j ≠ 0 при всех j = m+1, m+2, …, n.Здесь предполагается, что A_m+1, A_m+2, …, A_n небазисных столбцов.

Пример 6.        Z (Х) = 5х₁ - 2х₂ – 3х₃ + 0х₄ + 0х₅ + 0x₆ → min,

2x₁ + x₂ – x₃ + x₄ + 0x₅ + 0x₆ = 5,

3x₁ +2x₂ + x₃ +0x₄ + x₅ + 0x₆ = 7,

x₁ + 0x₂ – 3x₃ +0x₄ +0x₅ +x₆ = 4,

x_i ≥ 0, i = 1, 2, 3, 4, 5, 6.

Решение. 1)Составим симплексную таблицу.

№	Б	Сб	В	5	-2	-3	0	0	0
				A1	A2	A3	A4	A5	A6
1	A4	с4= 0	b1=5	2	1	-1	1	0	0	+
2	A5	с5= 0	b2=7	3	2	1	0	1	0	(1) (1) (3)
3	A6	с6= 0	b 3=4	1	0	-3	0	0	1	+
4			Z=0	-5	2	3	0	0	0

2) Матрица. А размера 3×6 имеет 3 базисных столбца А₄ = ,  А₅ = ,   А₆ =  .

3) Значения базисных переменных с теми же номерами, что имеют базисные столбцы, берутся равными соответствующим элементам столбца В, то есть  х₄= b₁=5,   х₅= b₂ =7,   х₆= b₃ =4.

Значения небазисных переменных берутся равными нулю, то есть  х₁ = х₂ = х₃ = 0.

4) Первоначальный план будет X₀=(х₁= 0,х₂ = 0, х₃ = 0, х₄ = 5, х₅ =7, х₆ = 4). Оптимальность плана X₀ можно проверить по значениям  ∆₁, ∆₂, ∆₃.

Эти оценки находятся по формуле: ∆_j = C_бA_j – c_j,  j = 1, 2, 3.

Если  ∆_j ≤ 0  при всех значениях  j = 1, 2, 3,  то текущий план Х₀ оптимален:  Х₀ = Х^*, и тогда

min Z(Х)=Z(Х₀)=Z(Х^*)= 5∙(0)–2∙(0) – 3∙(0) + 0∙(5) + 0∙(7) + 0∙(4) = 0.

Это число Z = 0  стоит внизу под столбцом В. Если же хотя бы одна оценка  ∆_j > 0,  то текущий план Х₀ не оптимален, его можно улучшить, то есть перейти к другому текущему плану Х₁, для которого значение Z(Х₁) окажется меньше, чем  Z = 0.Оценки базисных столбцов  А₄, А₅ и А₆  равны  ∆₅ = ∆₆ = ∆₇ = 0. Эти нули можно записывать в таблицу сразу, не вычисляя. Находим оценки небазисных столбцов  А₁, А₂ и А₃.

∆₁ = C_б∙A₁ – c₁ = (0; 0; 0)∙(2;3;1)–5 = (0)∙(2) + (0)∙(3) + (0)∙(1)–5 = 0 + 0 + 0 –5= -5 < 0,

∆₂ = C_б∙A₂ – c₂ = (0;0;0)∙(1;2;0) – (-2) =(0)∙(1) + (0)∙(2) + (0)∙(0)–(2) = 0 + 0 + 0 + 2 = 2 > 0,

∆₃ = C_б∙A₃ – c₃ = (0;0;0)∙(-1;1;-3) – (-3) = (0)∙(-1) + (0)∙(1) + (0)∙(-3)–(-3) =  0+0+0 – (-3) = 3 > 0.

5) Так как  ∆₂ = +2 > 0,  ∆₃ = +3 > 0, то текущий план Х₀ неоптимален. Для улучшения текущего плана Х₀  находим сначала θ_j для каждого столбца с положительной оценкой по формуле