Решение 1.Проверяем выполнение необходимого и достаточного
условия разрешимости задача: 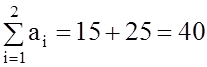 ,
, 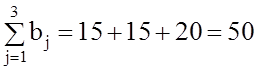 . Значит данная задача открытая.
. Значит данная задача открытая.
2.Введем фиктивного поставщика с запасами а3 = 50-40 = 10 и нулевыми стоимости перевозок единиц груза (см. табл. 16)
3.Находим первоначальное решение, например, методом минимального элемента. Заполнение фиктивного поставщика в последнюю очередь. Для удобства укажем последовательность заполнения таблицы поставок: х13 = 15, х22 = 15, х21 = 10, х31 = 5, х33 = 5.
Таблица 16
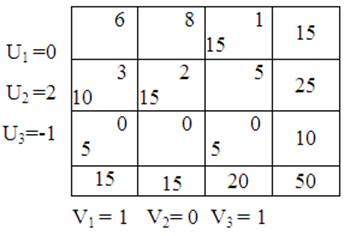
4.Находим матрицу оценок 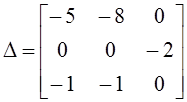 .
.
Так как Δij ≤
0 ![]() i,j, то план перевозок
i,j, то план перевозок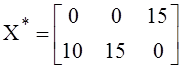
![]() оптимальный.
оптимальный.
Стоимость перевозок по оптимальному плану min Z(X) = Z(X*)=1·15+3·10+2·15=75.
6.1.7.Бесконечное множество оптимальных решений. В транспортной задаче существует множество оптимальных решений, если хотя бы одна оценка свободной клетки транспортной таблицы равна нулю.
Теорема. Пусть имеется транспортная задача, тогда: если ![]() - некоторые оптимальные
решения задачи, то
- некоторые оптимальные
решения задачи, то ![]() где t1+t2=1, t1≥
0, t2≥
0, также является оптимальным решением.
где t1+t2=1, t1≥
0, t2≥
0, также является оптимальным решением.
Пример 3. Найти оптимальное решение для транспортной задачи (табл. 17).
Таблица 17
|
2 |
6 |
5 |
55 |
|
3 |
4 |
6 |
20 |
|
40 |
10 |
25 |
Решение.1)Находим первоначальный план методом минимального элемента.
Заполняем таблицу следующим образом: х11=40, х22 = 10, х23 = 10, х13 = 15.
Таблица 18
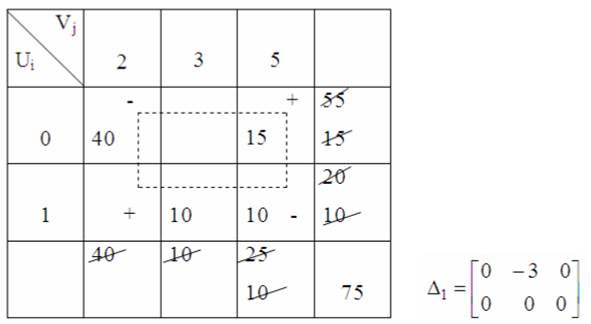 ,
,
|
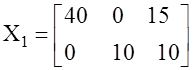 .
.
Все оценки клеток табл. 18 ∆ij
≤ 0, значит план ![]() оптимален.
оптимален.
![]()
Так как оценка свободной клетки (2, 1) нулевая, т.е. ∆21 = 0, то задача имеет не единственное решение. Для отыскания общего оптимального решения, прежде всего, необходимо перейти к следующему новому оптимальному решению.
3) ∆21 = 0 следует перемещать по циклу с замещением клетки (2, 1).
Находим θ1= ![]() {x11=40, x23=10
} =10, откуда находим второе оптимальное решение
{x11=40, x23=10
} =10, откуда находим второе оптимальное решение
Таблица 19
|
2 30 |
6 |
5 25 |
|
3 10 |
4 10 |
6 |
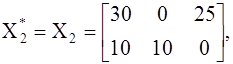
![]()
4) находим общее оптимальное решение ![]() , где t1 + t2 = 1, t1 ≥ 0, t2 ≥ 0.
, где t1 + t2 = 1, t1 ≥ 0, t2 ≥ 0.
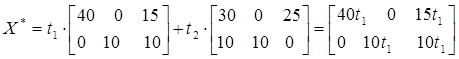
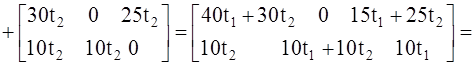
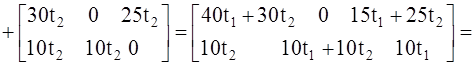
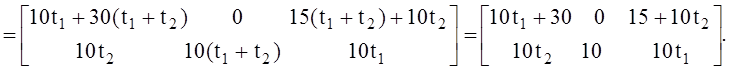
Таким образом, общее оптимальное решение 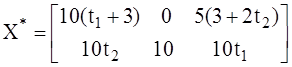 .
.
Задаваясь любыми значениями t1, t2 при сохранении условий t1 ≥ 0, t2≥ 0 и t1 + t2 = 1, будем получать различные оптимальные решения, а среди них и указанные выше оптимальные решения.
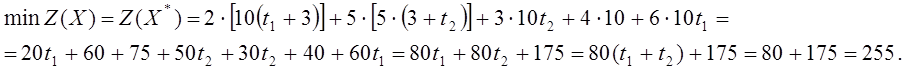
Решение транспортной задачи на ЭВМ. Исходные данные для транспортной задачи в таблице на рис. 1.
A |
B |
C |
D |
E |
|
|
1 |
2 |
1 |
1 |
||
|
2 |
3 |
2 |
1 |
||
|
3 |
1 |
2 |
3 |
||
|
4 |
2 |
4 |
5 |
||
|
5 |
|||||
|
6 |
=СУММ (А 6:С6) |
40 |
|||
|
7 |
=СУММ (А7: С 7) |
50 |
|||
|
8 |
=СУММ (А 8: С 8) |
30 |
|||
|
9 |
=СУММ (А 9: С9) |
70 |
|||
|
10 |
=СУММ (А6 : А 9) |
=СУММ ( В 6 : В 9) |
=СУММ (С 6 : С 9) |
=СУММПРОИЗВ (А1 : С4; А6 : С9) |
|
|
11 |
40 |
70 |
80 |
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.