Задача линейного программирования. Проверка оптимальности текущего плана, страница 19

3.Находим координаты т. А из решения системы уравнений

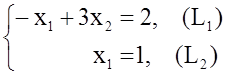
где т. А=(L₁)Ç(L₂). Отсюда А=(1,1), а Z_min =Z(A)= 3∙1+5∙1 = 8.

Следовательно, max Z(X) = +∞, min Z(X)=8 при Х^*=А=(1, 1).

Пример 9. Найти максимум и минимум функции Z=4x₁-6x₂+1  при ограничениях:

                                                                                     (1)

                                                                                  (2)

                                                                                 (3)

                                                                                             (4)

.                                                                                             (5)

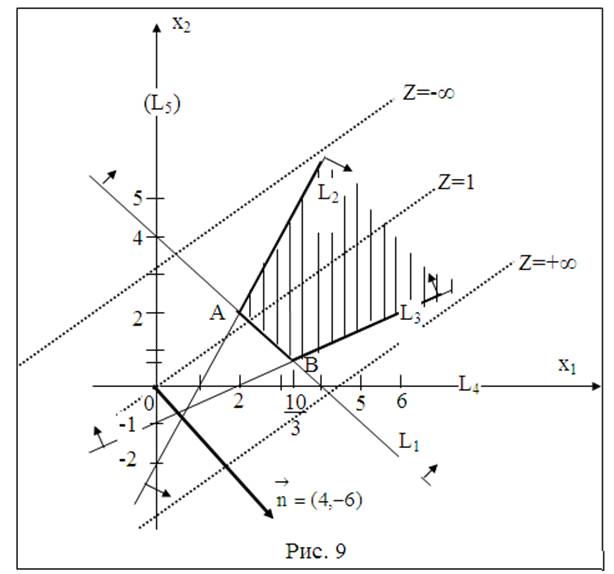
Решение.1.Строим прямые, уравнения, которых получаются в результате замены в ограничениях (1)…(5) знаков неравенств на знаки равенств (см. рис. 9).

2.Строим прямую Z = 1. Для этого строим вектор  и через т. О(0, 0) проводим прямую, перпендикулярную ему.

3. Перемещаем прямую в направлении противоположном вектору. Прямая Z всегда будет пересекать многоугольник решений. Следовательно, линейная функция неограниченно убывает, и конечного оптимума у нее нет, т.е. min Z = -∞.

4.Перемещаем прямую в направлении вектора. И в этом случае прямая Z всегда будет пересекать многоугольник решений. Следовательно, конечного оптимума отсутствует, т.е. mах Z = ∞.

Пример 10. Найти максимум и минимум функции Z=-2x₁+2x₂  при условиях:

                                                                                     (1)

                                                                                  (2)

                                                                                             (3)

.                                                                                             (4)

Решение.1.Строим прямую  (L₁), соответствующую ограничению (1). Не трудно заметить, что прямая проходит через точки (0,2) и (2,0) (см. рис. 10).

2.Строим прямую  (L₂), соответствующую ограничению (2). Эта прямая проходит через точки (0,1) и (-1,0).

3.Так как прямые (L₁) и (L₂) не проходят через точку О(0,0), подставляем координаты т. О в первое и второе ограничения.Получаем: 0≥2 и 0≥1. Это неверно, следовательно т.О не лежит в плоскости решений. Таким образом, стрелки на концах прямых (L₁) и (L₂) должны быть направлены в полуплоскость не содержащую т. О(0,0).

4.Строим прямую Z=0. Для этого строим вектор  и через т. О(0, 0) проводим прямую, перпендикулярную ему (см. рис. 10).

5.Перемещаем прямую Z в направлении вектора . Эта прямая встретит область решений в точке А=(L₁) Ç (L₂) (прямая Z совпадает с граничной прямой (L₂) области допустимых решений и проходит через одну угловую точку этой области А). Из рис. 10 видно, что прямая Z принимает минимальное значение в любой точке ,находящейся  в области решений, и лежит на прямой (L₂), начиная с т.А и заканчивая т. В. Для нахождения общего оптимального решения находим координаты т. А и координаты произвольной точки, лежащей на оптимальной части прямой (L₂).

6.Определяем координаты точки А=(L₁) Ç (L₂)

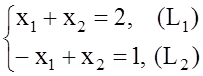
2х2 = 3

Определяем координаты, например т.С. Полагая в уравнении  (L₂),  (число 1 выбрано произвольно и больше 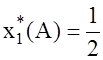), получим -1+х₂=1 Þ х₂=2; .

7.Вычисляем.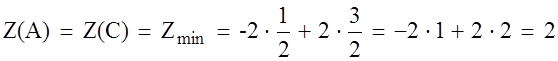

Согласно рис. 10 задача имеет бесконечное множество оптимальных решений

Х^* = (1-t) + t, 0 ≤ t ≤ ∞,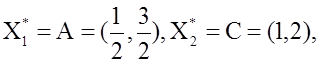 общая формула для определения любого оптимального решения задачи (общее решение) 

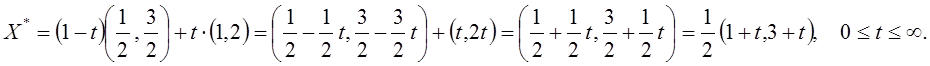
Придавая параметру t любые числовые значения от 0 до ∞, будем получать различные оптимальные решения задачи, при любом из которых  Z = Z_min = 2.

8.Перемещаем прямую Z в направлении ее возрастания (т.е. в направлении вектора ). В виду того, что в этом направлении область допустимых решений не ограничена, прямая уходит в бесконечность. Задача не имеет решения вследствие неограниченности целевой функции, т.е. max Z(X)= + ∞.