Задача линейного программирования. Проверка оптимальности текущего плана, страница 13

Решение. 1) Преобразуем расширенную матрицу

(-1)

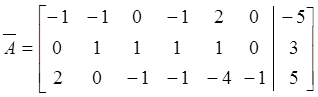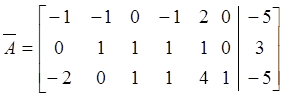            →      (1) →

(-1)

                      →

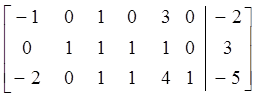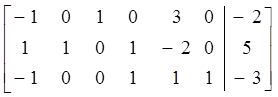
Теперь матрица  имеет три базисных столбца А₃, А₂, А₆.

2) Составим симплексную таблицу.

№	Б	Сб	В	3	5	-1	3	-6	0
				A1	A2	A3	A4	A5	А6
1	A3	-1	-2	-1	0	1	0	3	0	(-1)(1) (–1)
2	A2	5	5	1	1	0	1	-2	0	+
3	A6	0	-3	-1	0	0	1	1	1	+
4			27	3	0	0	2	-7	0

3) Находим отрицательные числа в столбце В  b₁ = -2 ,  b₃ = -3 .

4) Находим столбцы с положительными оценками. В нашей задаче такие столбцы А₁, А₄.

5) Столбец А₁ имеет несколько отрицательных элементов, поэтому находим θ₁ по формуле

θ₁ = 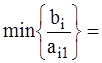 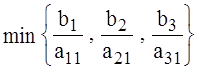,где min распространяется на отношения тех чисел b_i и a_ij, которые имеют одинаковые знаки.θ₁ = 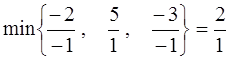 ,выгода V₁ = ∆₁. θ₁ = 3. 2 = 6 .

6) Столбец А₄ не имеет ни одного отрицательного элемента, поэтому отвергаем θ₄.

7) Значит, выгоднее сделать базисным столбец А₁ с ведущим элементом а₁₁ = -1 .

8) Запишем симплексную таблицу

№	Б	Сб	В	3	5	-1	3	-6	0
				A1	A2	A3	A4	A5	А6
1	A1	3	2	1	0	-1	0	-3	0
2	A2	5	3	0	1	1	1	1	0	+
3	A6	0	-1	0	0	-1	1	-2	1	(-1) (1)  (-1)
4			21	0	0	3	2	2	0

9) Находим отрицательные числа в столбце В.  В нашей таблице есть только один b₃ = -1.

10) Находим столбцы с положительными оценками. Таких в нашей таблице А₃, А₄ и А₅.

11) Столбец А₃ имеет отрицательные числа, поэтому находим θ₃.

θ₃ = 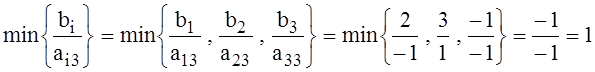 ,где min распространяется на отношения тех чисел b_i и a_i3 , которые имеют одинаковые знаки. Выгода V₃ = ∆₃ θ₃ = 3∙1 = 3 .

12) Столбец А₄ не имеет ни одного отрицательного элемента, поэтому отвергаем θ₄.

13) Столбец А₅ имеет два отрицательных элемента, поэтому находим θ₅ .

θ₅ = 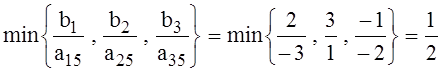 ,выгода V₅=∆₅ θ₅=2 ∙ =1 .

14) Значит, выгоднее сделать базисным столбцом А₃ с ведущим элементом а₃₃= -1.

15) Запишем симплексную таблицу.

№	Б	Сб	В	3	5	-1	3	-6	0
				A1	A2	A3	A4	A5	А6
1	A1	3	3	1	0	0	-1	-1	-1
2	A2	5	2	0	1	0	2	-1	1
3	A3	-1	1	0	0	1	-1	2	-1
4			18	0	0	0	5	-4	3