Задача линейного программирования. Проверка оптимальности текущего плана, страница 11

3х₁ + 2х₂ + 0х₃ = 25 , х₁ ≥ 0 ,  х₂ ≥ 0 ,  х₃ ≥ 0 .

Решение. 1) Введем х₄ ≥ 0  в левую часть равенства  -2х₁ – x₂ + 0x₃ = 10.

2) Введем х₅ ≥ 0  в левую часть равенства  3х₁ + 2х₂ + 0x₃ = 25

Данная задача – задача на максимум, поэтому х₄ и х₅ в целевую функцию вводятся с коэффициентом – М.

Z(X) = - 3x₁ + x₂ + 0x₃ – Mx₄ – Mx₅  → max , х₁ – 2х₂ + х₃ + 0x₄ + 0x₅ = 10 ,

-2х₁ – х₂ + 0х₃ + 1∙x₄ + 0x₅ = 10 ,                                                   

3х₁ + 2х₂ + 0х₃ + 0x₄ + 1∙x₅ = 25 х_i ≥ 0 ,  i = 1, 2, 3, 4, 5 .

2)  Составим симплексную таблицу.

№	Б	Сб	В	-3	1	0	-М	-М
				A1	A2	A3	A4	A5
1	A3	0	10	1	-2	1	0	0
2	A4	-М	10	-2	-1	0	1	0
3	A5	-М	25	3	2	0	0	1	(1/2) (1/2) (1)
4			-35М	М+3	-М-1	0	0	0

Так как М – большое положительное число, то Z = - 35M < 0, Δ₁ = - M + 3 < 0, ₂ = - M - 1 < 0.

Произведем необходимые вычисления:

θ₁ < 0,

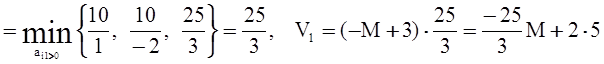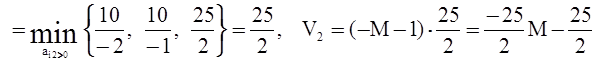θ₂< 0.

Так как   то выгоднее включить в базис столбец А₂. При этом ведущим элементом будет а₃₂ = 2.

3)  Составляем новую таблицу

№	Б	Сб	В	-3	1	0	-М	-М
				A1	A2	A3	A4	A5
1	A3	0	35	4	0	1	0	1
2	A4	-М	45/2	-1/2	0	0	1	1/2
3	A2	1	25/2	3/2	1	0	0	1/2
4					0	0	0

Так как Δ_i ≥ 0 при всех i=1, 2, 3, 4, 5 и 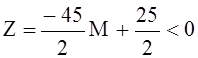 , то исходная задача не имеет опорного плана.

1.2.9. Решить задачу ЛП, если система ограничений имеет базис, но среди свободных планов есть отрицательные.

Пусть в уравнениях      a_i1x₁ + a_i2x₂ + … + a_inx_n = b_i,    i=1, 2, …, m,                                                                                                     (1)

существует b_i < 0. Умножим уравнение (1) на (-1). Тогда новый свободный член (-b_i) уже положителен. Однако если исходная система имела базис, то после смены знака в (1) столбец, в котором в i-ой строке стояла единица, перестает быть базисным: на месте 1 появляется (–1). Это можно преодолеть, применяя далее к задаче с неотрицательными свободными членами и с недостатком базисных столбцов метод искусственного базиса.Можно, однако, предложить менее трудоемкий способ. В исходной системе с базисом, но с некоторыми отрицательными свободными членами, отметим те строки, в которых b_i < 0.

°1) Если в какой-нибудь из таких строк все дальнейшие элементы строки a_ij положительны, то ни при каких неотрицательных x_j равенство a_{i 1}x₁ + a_i2x₂ + … + a_inx_n = b_i  вообще не может выполняться, так как левая часть неотрицательна, а правая отрицательна, то есть, в этом случае решения нет.

Пример 13.  Z (Х) = 2х₁ – 3х₂ + 1          min, х₁ + х₂ ≤ 4, х₁ + х₂ ≤ -1, х₁ + 2х₂ ≤ 1,

x_i ≥ 0, i = 1, 2.

Решение. 1) Запишем задачу в основном виде:

Z (Х) = 2х₁ – 3х₂ + 0х₃ + 0х₄ + 0х₅ + 1          min, х₁ + х₂ + х₃ + 0х₄ + 0х₅ =  4, х₁ + х₂ + 0х₃ + х₄ +0х₅ = -1, х₁ + 2х₂ + 0х₃ + 0х₄ + х₅ = 1,

x_i ≥ 0,  i = 1, 2, 3, 4, 5.