Задача линейного программирования. Проверка оптимальности текущего плана, страница 23

Заполняем, например, клетки (1, 2) и (1, 3) (табл. 6).

Таблица 5                                                Таблица 6

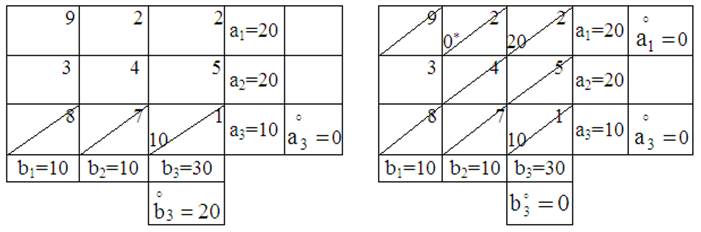
5) Заполняем клетку (2, 1), где стоит минимальный элемент в оставшейся табл. 6 по формуле: х₂₁ =

6) Закроем первый столбец (где нет остатка).

7) Находим остатки второй строки   = а₂ – х₂₁ = 20 – 10 = 10  (табл. 7).

8)Заполняем последнюю свободную клетку(2,2) Х₂₂=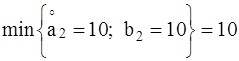 (табл. 8).

Таблица 7                                             Таблица 8

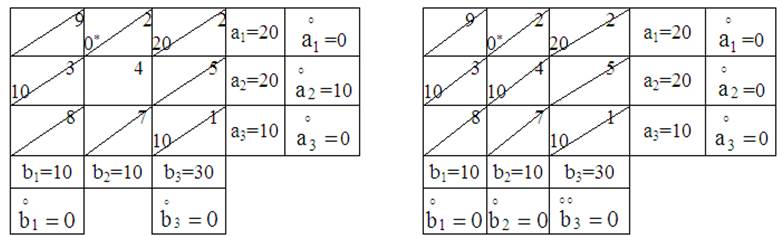
9) Проверяем правильность построения первоначального решения.

В табл. 8 m+n-1 = 3+3-1=5 занятых клеток.

10) Первоначальный план методом минимального элемента равен

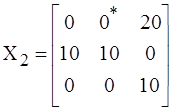.                                                                           (8)

11)Вычислим первоначальную стоимость перевозок (см. табл. 8)

Z(X₂) = 2·0^* + 2·20 + 3·10 + 4·10 + 1·10 = 120.

Поиск оптимального плана. Проверим оптимальность первоначального плана Х₁ методом потенциалов следующим образом.

Первый способ

1) Каждой строке из табл. 4 сопоставим переменную U_i, называемую потенциалом поставщика.

2) Каждому столбцу из табл. 4 сопоставим переменную Vj, называемую потенциалом потребителя.

3) Оценкой клетки (i;j) назовем число ∆_ij= U_i+ V_j-с_ij, (10), где с_ij – стоимость перевозки, соответствующая данной клетке.

4) Потребуем, чтобы для заполненных клеток оценка равнялась нулю, т.е.

∆₁₁= U₁+V₁-с₁₁= U₁+V₁-9=0 => U₁+V₁=9, ∆₁₂= U₁+V₂-с₁₂= U₁+V₂-2=0 => U₁+V₂=2,

∆₂₂= U₂+V₂-с₂₂= U₂+V₂-4=0 => U₂+V₂=4, ∆₂₃= U₂+V₃-с₂₃= U₂+V₃-5=0 => U₂+V₃=5,

∆₃₃= U₃+V₃-с₃₃= U₃+V₃-1=0 => U₃+V₃=1.

5) Полагаем U₁=0, находим V₁=9; V₂=2; U₂=+2; V₃=3; U₃=-2.

Аналогично можно проверить оптимальность  методом потенциалов.

6) Находим оценки для свободных клеток таблицы 4 и проверим оптимальность текущего плана X₁ по значения этих оценках. Если для всех свободных клеток ∆_ij≤0, то текущий план оптимален. Если хотя бы одна из оценок положительна (∆_ij>0), то план можно улучшить.

∆₁₃= U₁+V₃-с₁₃=0+3-2=1>0, ∆₂₁= U₂+V₁-с₂₁=2+9-3=8>0,∆₃₁= U₃+V₁-с₃₁=-2+9-8=-1<0,

∆₃₂= U₃+V₂-с₃₂=-2+2-7=-7<0. Так как ∆₁₃=1>0, ∆₂₁=8>0, то план X₁ не оптимален.

7) Находим свободную клетку в таблице 4 с максимальной положительной оценкой: max {∆₁₃=1, ∆₂₁=8} =8.

8) Для клетки (2,1), которой соответствует наибольшая оценка, ставим знак «+» и строим цикл (закрытый путь), начинающийся и заканчивающийся в этой клетке (см. табл.9).

Примеры некоторых циклов:

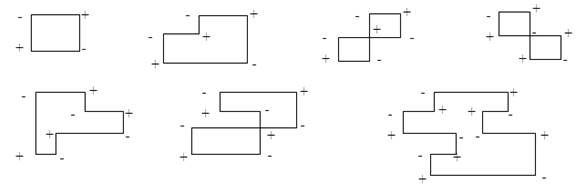
Рис. 1

Таблица 9                                         Таблица 10

                  

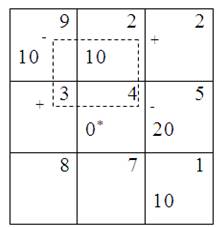
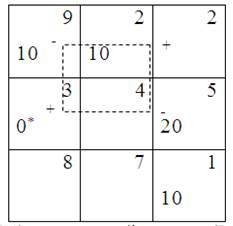
Следуя этому циклу, расставим чередующиеся знаки + и – в его вершинах, начиная с того знака +, что уже стоит в вершине (2,1).

9) Из объемов перевозок в тех клетках, что отмечены знаком «-», то есть из величин x₁₁=10 и x₂₂=0٭, выбираем меньший объём: θ₁= {x₁₁=10, x₂₂=0٭} =0٭.

10) Вычитаем 0٭ в тех клетках, что помечены минусом, а прибавляем 0٭ в тех клетках, что помечены плюсом.

Получаем новый план. Клетка (2,1) стала занятой, а клетка (2,2) – свободной (см. табл. 10).

11) Проверим оптимальность нового плана. Определим оценки свободных клеток, исходя из системы:

∆₁₁= U₁+V₁-с₁₁= U₁+V₁-9=0 => U₁+V₁=9,  ∆₁₂= U₁+V₂-с₁₂= U₁+V₂-2=0 => U₁+V₂=2,

∆₂₁= U₂+V₁-с₂₁= U₂+V₁-3=0 => U₂+V₁=3, ∆₂₃= U₂+V₃-с₂₃= U₂+V₃-5=0 => U₂+V₃=5,

∆₃₃= U₃+V₃-с₃₃= U₃+V₃-1=0 => U₃+V₃=1.

Положим U₁=0, находим V₁=9; V₂=2; U₂=-6; V₃=11; U₃=-10.

Теперь находим оценки свободных клеток.∆₁₃= U₁+V₃-с₁₃=0+11-2=9>0,

∆₂₂= U₂+V₂-с₂₂=-6+2-4=-8<0, ∆₃₁= U₃+V₁-с₃₁=-10+9-8=-9<0,∆₃₂= U₃+V₂-с₃₂=-10+2-1=-9<0.

Так как ∆₁₃=9>0, то текущий план не оптимален.

12) Делаем занятой клетку (1,3), отмечая её знаком «+».

13) Находим в таблице 12 цикл: (1,3)→(2,3)→(2,1)→(1,1)→(1,3).

14) Расставляем знаки, начиная с уже поставленного знака«+».

15) Находим минимальный объём перевозки для клеток, отмеченных знаком «-».