В столбце В уже нет отрицательных чисел, значит предварительный этап завершен, и дальше нужно продолжать вычисление обычным симплекс-методом. Дальнейшее решение предоставляем выполнить самостоятельно в соответствии с алгоритмом, изложенным в разд.II.
Ответ: min Z(X) = 12, при Х* = (5, 0, 3, 0, 0, 2).
Замечание. Можно решать пример 15 без преобразования исходной матрицы. Если сменить знак в втором уравнении, чтобы все свободные члены стали положительными, то затем можно применить метод искусственного базиса.
1.3. Решение задачи (ЛП) на ЭВМ (MSExcel)
пример 19 .Z(X) = 5x1 – 2x2 – 3x3 → min ,
2x1 + x2 – x3 ≤ 5 ,
3x1 +2x2 + x3 ≤ 7 ,
x1 – 3x3 ≤ 4 ,
x1 ≥ 0; x2 ≥ 0; x3 ≥ 0.
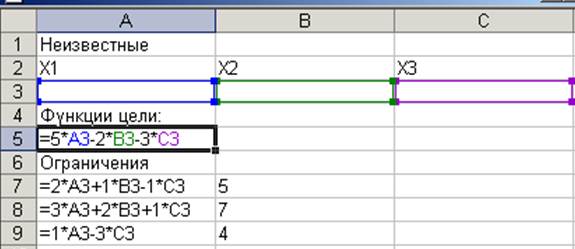
Рис. 1. Структура рабочего листа
1. В ячейки А2:С2 введем X1, Х2 и Х3.
2 .Отведем А3, В3 и С3 под значения неизвестных X1, Х2 и Х3.
3.В ячейку А5 введем функции цели = 5*А3 – 2*В3 – 3*С3
4.В ячейки А7:А9 введем левые части ограничений: = 2* А3 + 1*В3 – 1*С3, = 3* А3 + 2*В3 + 1*С3,= 1* А3 – 3*С3
5.В ячейки В7:В9 введем правые части ограничений.
6.Выберем команду Сервис, Поиск решения (рис. 2).
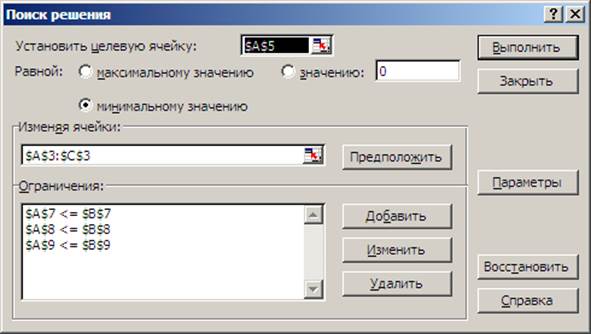
Рис. 2. Диалоговое окно Поиск решения
Замечание. Если в Сервис нет окна Поиск решения, тогда выберем команду Сервис, над строкой, в окне надстройки включим Поиск решения, нажмем ок. Если в окне настройка нет элемента поиск решения, то нажимаем кнопку обзор, чтобы самостоятельно найти файл поиск решения.
7.В окне Поиск решения в поле Установить целевую введем $A$5.
8.В группе переключателей выберем минимальное значение.
9.В поле Изменяя ячейки введем $A$3; $C$3.
10.Щелкнем кнопку Добавить.
11.В блоке Добавление ограничения установим первое ограничение.
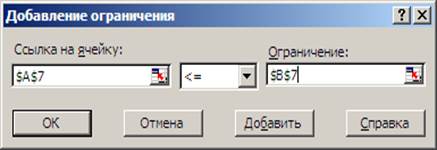
Рис. 3.Диалоговый блок Добавление ограничения
а) введем ссылку на ячейку с формулой $A$7; б) выберем оператор <=;
в) введем в поле ограничение: $B$7.
12.Щелкнем кнопку Добавить и зададим второе ограничение а) $A$8; б) <=; в) $B$8.
13.Щелкнем кнопку Добавить и зададим третье ограничение а) $A$9; б) <=; в) $B$9.
14.Нажмем ok в блоке Добавление ограничения.
15.Щелкнем кнопку Параметры (рис. 4) и включим: а) Линейная модель;
б) Неотрицательные значения; в) Автоматическое масштабирование. Нажмем ok.
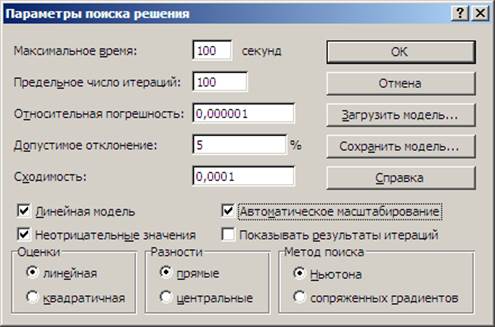
Рис. 4. Диалоговое окно Параметры поиска решения
16.В окне Поиск решения нажмем кнопку Выполнить, программа выведет результаты решения (рис.5).
17.В окне Результаты поиска решения предложим Excel сохранить найденные значения (рис. 6).
18.Нажмем ok.
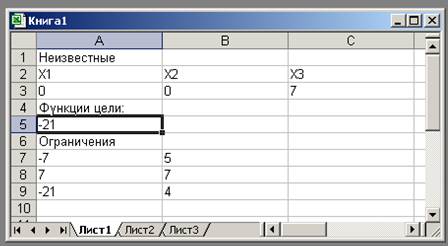
Рис. 5. Оптимальное решение задачи
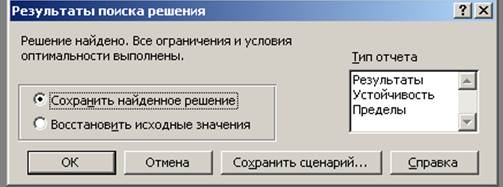
Рис. 6. Окно Результаты поиска решения.Глава 2. Графическое решение Задачи ЛП
2.1.Задача с двумя переменными .Дана задача линейного программирования
![]() ,
(1)
,
(1)
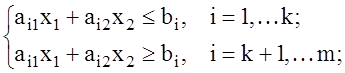 (2)
(2)
в которую входят только два неизвестных х1 и х2. Каждое из неравенств системы (2) определяет на координатной плоскости (х1, х2) некоторая полуплоскость. Следовательно, допустимое множество решения задачи (1)-(2) есть пересечение конечного числа полуплоскостей, т.е. некоторая многоугольная область на плоскости (х1, х2).
При использовании графического метода используется линия уровня.
Линией уровня функции Z(X)
= Z(х1, х2)
называется множество всех точек (х1, х2), в которых функция принимает постоянное
значение, т. е. Z(X) = const. В случае
линейной функции ![]() все линии уровня являются прямыми,
перпендикулярными общему вектору
все линии уровня являются прямыми,
перпендикулярными общему вектору ![]() определяемому соотношением
определяемому соотношением
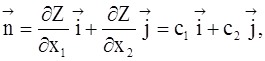 где
где ![]() и
и ![]() - орты всей х1 и х2 соответственно.
Координатами вектора
- орты всей х1 и х2 соответственно.
Координатами вектора ![]() являются коэффициенты целевой
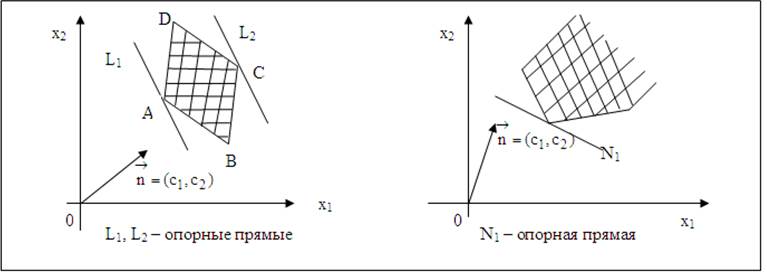
функции Z(X). Опорной прямой называется
линия уровня, которая имеет хотя бы одну общую точку с областью решений и по
отношению, к которой эта область находится в одной из полуплоскостей. Значения
целевой функции на линиях уровня возрастают, если линия уровня перемещать в
направлении их нормали, и убывают
при перемещении линий уровня в противоположном направлении.
являются коэффициенты целевой
функции Z(X). Опорной прямой называется
линия уровня, которая имеет хотя бы одну общую точку с областью решений и по
отношению, к которой эта область находится в одной из полуплоскостей. Значения
целевой функции на линиях уровня возрастают, если линия уровня перемещать в
направлении их нормали, и убывают
при перемещении линий уровня в противоположном направлении.
2.1.1. Алгоритм решения задачи.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.