Задача линейного программирования. Проверка оптимальности текущего плана, страница 7

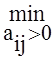
 θ_j =    , j= 2, 3 , i = 1, 2, 3.

θ₂ =   =

 

θ₃ =  =  .

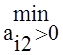
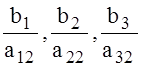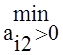
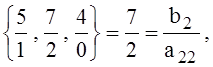
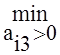
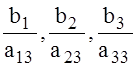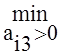
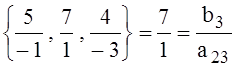6) Выгода V_j,  j = 2, 3 находится по формуле  V_j = ∆_j∙ θ_j,     j = 2, 3.

V₂ = ∆₂∙ θ₂ = 2∙ (  ) = 7;       V₃ = ∆₃∙ θ₃ = 3∙ (  ) = 21.

Так как V₃ > V₂, выгоднее включить в базис столбец А₃, при этом ведущим элементом будет  а₂₃ = 1. Обводим  а₂₃ = 1 кружком во второй строке. В столбце Б вместо А₅ запишем А₃. В столбце С_б заменим коэффициент  с₅ = 0  на  с₃ = -3. Поделим все элементы 2-ой строки, начиная со столбца В и до конца, на ведущий элемент а₂₃ = 1.

К первой строке прибавим вторую, а к третьей – вторую, умноженную на 3.

Замечание. В задаче на минимум V_К1>0, V_К2>0, …, V_Кs>0, выгода находится по формуле V = max{V_К1, V_К2, …, V_Кs}.В задаче на максимум V_К1<0, V_К2<0, …, V_Кs<0, выгода находится по формуле  V = max{|V_К1|, |V_К2|, …, |V_Кs|}.

Запишем симплексную таблицу.

№	Б	Сб	В	5	-2	-3	0	0	0
				A1	A2	A3	A4	A5	A6
1	A4	с4=0	b1=12	5	3	0	1	1	0
2	A3	с3= -3	b2=7	3	2	1	0	1	0
3	A6	с6=0	b3=25	10	6	0	0	3	1
4			Z= -21	-14	-4	0	0	-3	0

Значения базисных переменных в новой таблице равны х₄ =b₁=12, х₃=b₂ =7,х₆ =b₃= 25.

Значения небазисных переменных берутся равными нулю, т. е. х₁=х₂=х₅=0.

7) Текущий план по новой таблице Х₁ =(х₁ = 0, х₂ = 0, х₃ = 7, х₄ = 12, х₅ = 0, х₆ = 25).

8) Значение целевой функции в новой таблице равно Z(X) = С_б. В = (0; -3; 0) ∙ (12; 7; 25) = 0∙(12) + (-3)∙(7) + 0∙(25) = -21.

9) Вычислим  ∆_j,   j = 1, 2, 3, 4, 5, 6   в новой таблице.

Оценки базисных столбцов равны нулю: ∆₃ = 0,  ∆₄ = 0,  ∆₆ = 0.

Оценки остальных столбцов считаем по формуле:  ∆_j = С_б.∙A_j – c_j;

∆₁ = (0; -3; 0) ∙ (5; 3; 10) – 5 = 0∙5 + (-3)∙3 + 0∙10 – 5 = -14 < 0,

∆₂ = (0; -3; 0) ∙ (3; 2; 6) – (-2) = 0∙3 + (-3)∙2 + 0∙6 + 2 = -4 < 0,

∆₅ = (0; -3; 0) ∙ (1; 1; 3) – 0 = 0∙1 + (-3)∙1 + 0∙3 – 0 = -3 < 0.

10) Так как ∆_j ≤ 0   при   j = 1, 2, 3, 4, 5, 6,  значит, текущий план оптимален и Х^* = Х₁ = (0; 0; 7; 12; 0; 25),  а минимальное значение функции  Z(Х)  равно  min Z(Х) = -21.

11) Так как для всех небазисных столбцов А₁, А₂, А₅ оценки  ∆_j ≠ 0;

j = 1, 2, 5, значит оптимальный план Х^* = X₁ является единственным.

1.2.6. Бесконечное множество оптимальных решений

В задаче на минимум или на максимум существует бесконечное множество оптимальных решений, если же хотя бы одна оценка небазисных столбцов равна нулю, т.е. существует ∆_к=0; к = m+1, или m+2, …, или n,  где A_m+1, A_m+2, …, A_n небазисных столбцов.

Теорема 3. Пусть имеется основная задача ЛП, тогда:

1) Если Х₁º, Х₂º - некоторые допустимые решения задачи, то

Хº = (1 – t) Х₁º + t Х₂º, где 0 ≤ t ≤1, также является допустимым решением.

2) Если Х₁^*, Х₂^* – некоторые оптимальные решения задачи, то

Х^* = (1- t) X₁^* + t X₂^*, где 0 ≤ t ≤ 1, также является оптимальным решением.

Пример 7.        Z (Х) = 5х₁ → min,         х₁ – х₃ = 2 , х₃ + х₄ = 2 , х₂ – х₅ = 2 , х₅ + х₆ = 2 ,

x_i ≥ 0; i = 1, 2, 3, 4, 5, 6.

Решение. 1) Составим симплексную таблицу.