Задача линейного программирования. Проверка оптимальности текущего плана, страница 5

12) Значения базисных переменных в новой таблице равны

x₄ =b₁=4/3 , x₃ = b₂=23/3, x₂ = b₃=14/3

13) Значения небазисных переменных берутся равными нулю, т. е. х₁ = 0 .

14) Текущий план по новой таблице.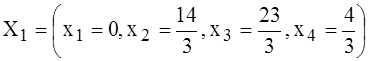

15) Значение целевой функции в новой таблице равно

 .

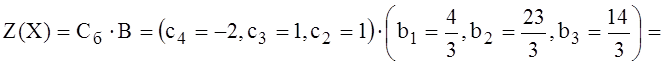
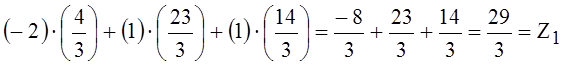16) Вычислим ∆_j, j = 1, 2, 3, 4 в новой таблице. Оценки базисных столбцов равны нулю: ∆₂=0, ∆₃=0, ∆₄=0. Оценки остальных столбцов считаем по формуле:           ∆_j = C_б ∙ A_j – c_j;

.

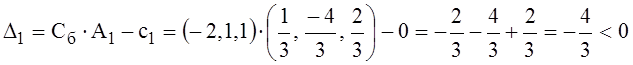17) Так как ∆_j ≤ 0 при j=1, 2, 3, 4, значит текущий планоптимален: 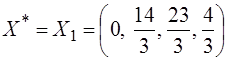, а минимальное значение функции Z(X) равно    min Z(X) = Z(X₁) = 29/3. 

18) Проверка:

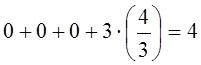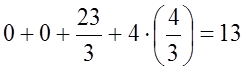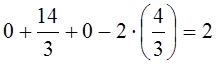, , , х₁ = 0 ,   х₂ =  14/3>0,   х₃ = 23/3>0,   х₄ = 4/3>0.

.

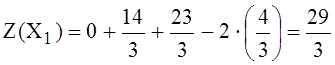Пример 5. Z(X) = -x₁ + x₂ + x₃ → max,

x₁ + 0x₂ + 0x₃ - 6x₄ – x₅ = 1,

0x₁ + x₂ + 0x₃ + x₄ + x₅ = 1,

0x₁ + 0x₂ + 1x₃ - 3x₄ – 4x₅ = 2,

x_i ≥ 0, i = 1, 2, 3, 4, 5.

Решение. 1) Составим симплексную таблицу.

№	Б	Сб	В	c1=-1	c2=1	c3=1	c4=0	c5=0
				A1	A2	A3	A4	A5
1	A1	с1= -1	b1=1	1	0	0	-6	-1
2	A2	c2= 1	b2=1	0	1	0	1	1
3	A3	с3= 1	b3=2	0	0	1	-3	-4
4			Z=2	∆1=0	∆2=0	∆3=0	∆4=4	∆5=-2

2) Находим базисные столбцы матрицы ограничений. А₁ = ,  А₃ = ,   А₃ =  .

3) В столбце Б симплексной таблицы запишем базисные столбцы А₁, А₂ и А₃ так, что в столбце А_i единица стоит на i-ом месте.

4) В столбце С_б симплексной таблицы запишем коэффициенты целевой функции Z(X), номера которых совпадают с номерами базисных столбцов этой строки.

5) В столбце В запишем свободные члены  b₁ = 1, b₂ =1, b₃=2.

6) Сверху над столбцами А₁, А₂, А₃, А₄ и А₅ запишем коэффициенты целевой функции с₁=-1, с₂=1, с₃=1, с₄=0 и с₅=0.

7) В столбцах А₁, А₂, А₃, А₄ и А₅ запишем столбцы матрицы А.

8) В строке 4 запишем текущее значение Z целевой функции, а также оценки ∆₁, ∆₂, ∆₃, ∆₄. и ∆₅.

9)Находим Z по формуле:Z(Х)=С_бВ=(с₁=-1,с₂=1,с₃=1)(b₁=1,b₂=1,b₃=2)=(-1)(1)+(1)(1)+(1)(2)= 2.

10) Находим оценки небазисных столбцов (∆₄, ∆₅) по формуле:∆_j =С_б А_j–с_j ;j=4,5. ∆₄ = С_б А₄ – с₄ = (-1, 1, 1) (-6, 1, -3) – 0 = 6 + 1 - 3 = 4 > 0. ∆₅ = С_б А₅ – с₅ = (-1, 1, 1) (-1, 1, -4) – 0 = 1 + 1 - 4 = -2 < 0

.Для базисных столбцов А₁, А₂, А₃  оценки равны  ∆₁ = ∆₂ = ∆₃ = 0.

11) Первоначальное решение, соответствующее этой таблице X₀ = (1, 1, 2, 0, 0).

12) Так как данная задача на максимум и ∆₅ = -2 < 0, значит текущий план не оптимален.

13) Для улучшения текущего плана Х₀ находим сначала θ₅ для столбца А₅ с отрицательной оценкой по формуле

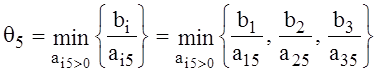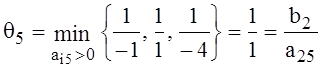 ; ; а₂₅=1 – ведущий элемент преобразования.

14) Обводим  а₂₅=1  кружком во второй строке.

15) В столбце Б вместо А₂ запишем А₅.

16) В столбце С_б заменим  с₂= 1  на с₅ = 0.

17) К первой строке прибавим вторую.

18) К третьей строке прибавим вторую, умноженную на 4.

19) Запишем вторую симплексную таблицу.