Задача линейного программирования. Проверка оптимальности текущего плана, страница 20

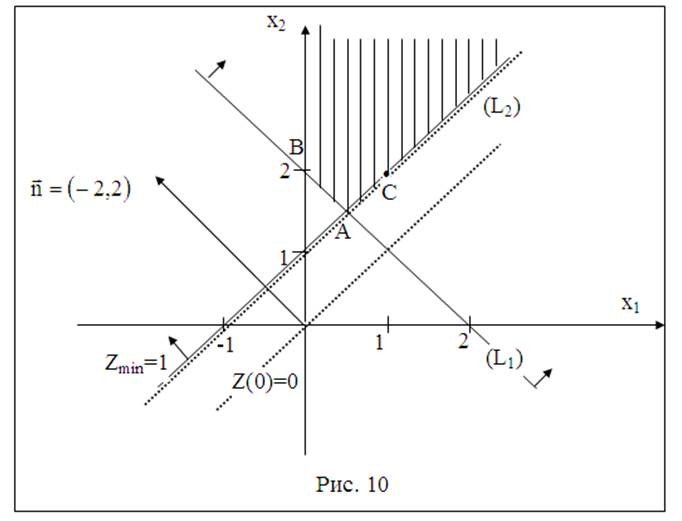
2.1.5. Отсутствие решения задачи. Задача не имеет решения в случае, когда область допустимых решений пустое множество, т.е. система ограничений несовместна.

Пример 11. Найти максимум и минимум функции Z=9x₁+x₂ при условиях:

                                                                                   (1)

                                                                                     (2)

                                                                                             (3)

                                                                                             (4)

.                                                                                             (5)

Решение. Строим область допустимых решений задачи. Для этого строим прямые линии, соответствующие неравенствам системы ограничений и находим полуплоскости, являющиеся областями решений этих неравенств (см рис.11). Область допустимых решений задачи является пустым множеством. Задача не имеет ни одного решения в виду несовместимости системы ограничений.

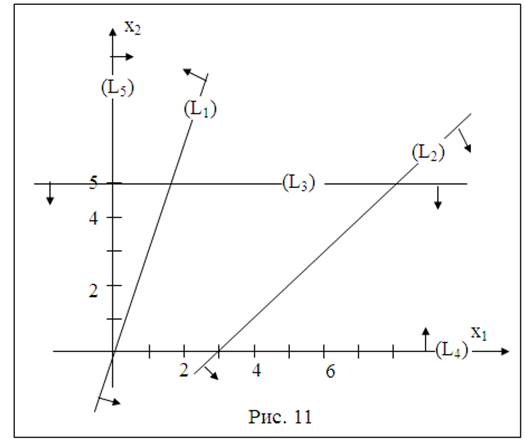
Упражнения. Решить графическим методом задачи

1) max (min) Z(X) = -(x₁ +x₂),  2) max (min) Z(X) = 2x₁ - 2x₂,    

x₁ + x₂ ≤ 3,                                 x₁ + x₂ ≤ 3,

x₁ + x₂ ≥3,                                   x₁ + x₂ ≥ 3,

x₁ - x₂ ≥ 2.                                                                         

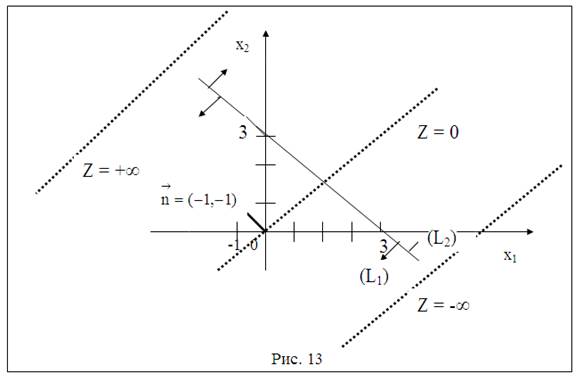
Читателю предлагается выполнить самостоятельно и убедиться, что Задача 1. не имеет решения вследствие неограниченности целевой функции, т. е. max Z(X) = +∞,min Z(X) = - ∞.

Задача 2.имеет единственное оптимальное решение Х^* = () при этом  max Z(X) = -4,

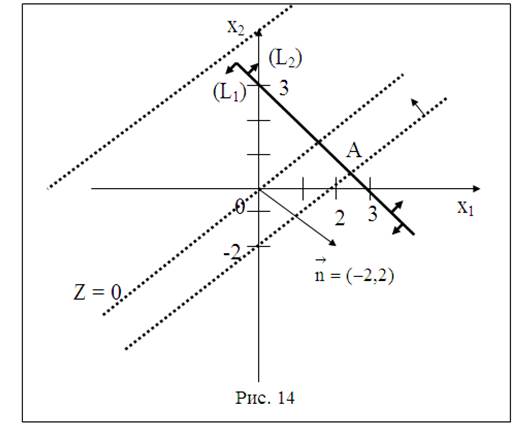
а не имеет решения вследствие неограниченности целевой функции, т.е. min Z(X) = - ∞.

2.3. Графическое решение Задачи (ЛП) с двумя переменными на ЭВМ

Пример 17.

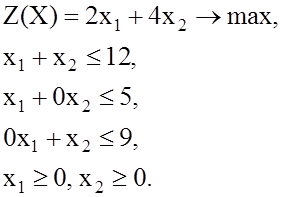
Решение.1.Вводим в ячейку А1 значение 0.

2.В ячейку А2 вводим значение, увеличенной на 0,2. Выделяем ячейки

А1:А2 и затем способом «автозаполнение» заполняем диапазон А1:А26.

Замечание. Способ «автозаполнение», берем мышкой (щелчок ЛКМ, по кнопке не отпускать) маркер заполнения рамки выделенного диапазона А1:А2, когда он примет вид +, и перемещаем его внизу, пока не появится цифра 5.

3. В ячейку В1 вводим формулу = 12 - А1. Далее способом «автозаполне-ние» формируем диапазон В1:В26.

4. Вводим в ячейку С1 формулу целевой функции = (2-2*А1)/4, соответствующей значению равно Z=2. Затем также как в предыдущем случае заполняем диапазон С1:С26.

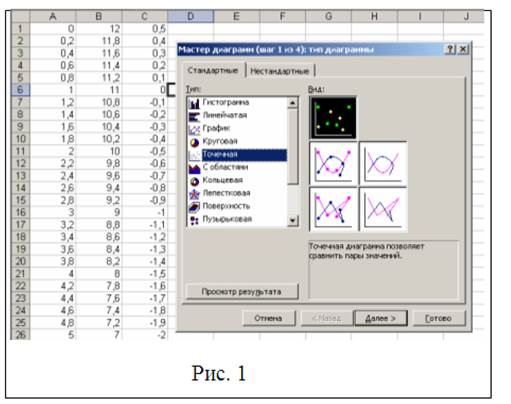
5.Выделяем диапазон ячеек А1:С26 и строим диаграмму с помощью команды Вставка→Диаграмма или с помощью соответствующей кнопки на панели инструментов программы Excel. В диалоговом окне «Мастер диаграмм» выбираем точечный тип диаграммы. Нажав на кнопку «Просмотр результата» и не отпуская ее, можно убедиться в правильности выбора типа диаграммы (рис. 1) .Нажав на кнопку «Далее» приходим ко второму диалоговому окну и в поле «Имя» вводим формулу х₁+х₂=12. Нажав кнопку «Добавить»  в тоже поле вводим формулу 2х₁+4х₂=2 (рис. 2).

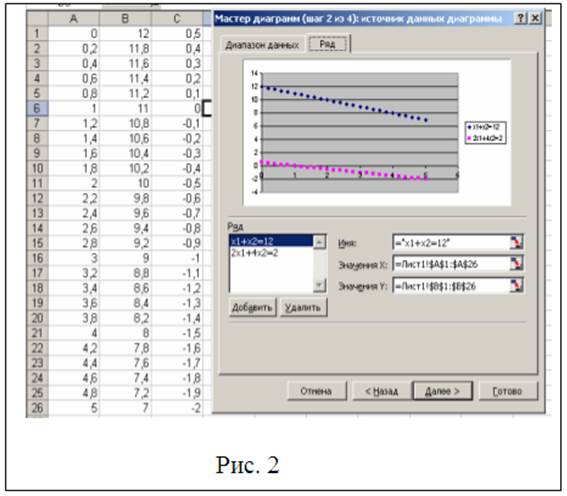
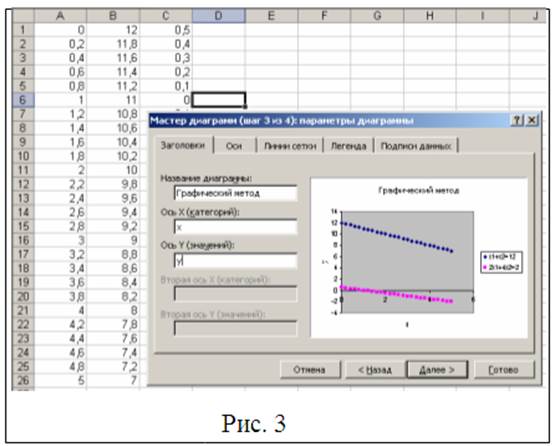
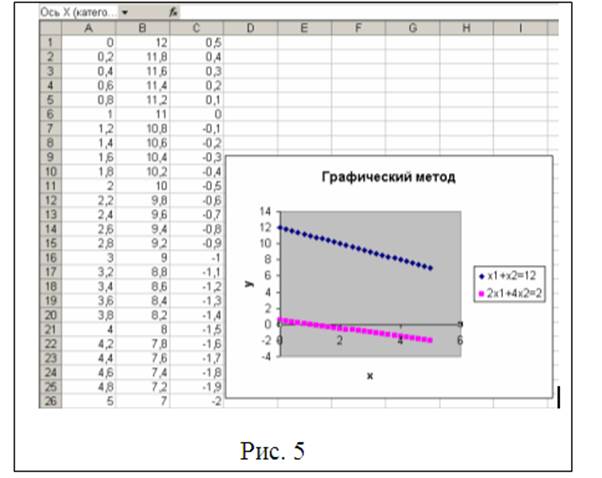
На третьем шаге нужно убрать линии сетки с помощью вкладки «Сетка»,на вкладке «Заголовки» в поле «Название диаграммы» введем Графический метод и выставим названия осей как представлено на рис. 3. Перейдя к последнему шагу построения диаграммы, выставим параметры как представлено на рис. 4.Нажав на кнопку «Готово» получим график представленный на рис. 5.

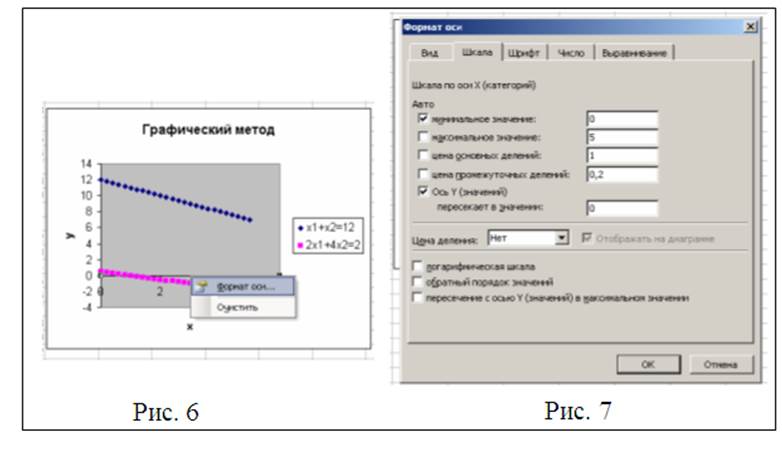
Настроим оси графика так, как представлено на рис. 7 для оси ОХ и рис. 8 для оси ОY. Для этого вызываем контекстное меню для каждой из указанных осей. В результате должно появиться изображение представленное на рис. 9. Из рис. 9 на котором представлено найденное решение видно, что точкой выхода целевой функции из области допустимых решений является точка с координатами (3, 9). Ответ: (3, 9), max Z = 42.

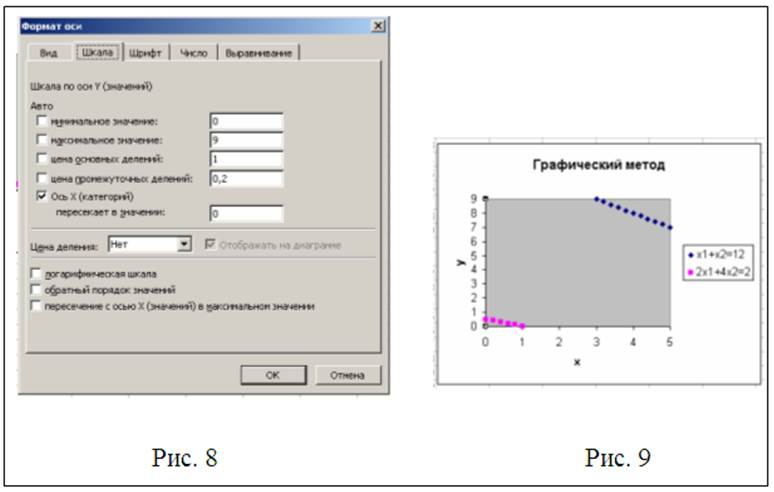
Пример 18.

Решение.1. Вводим в ячейку А1 значение 0.