смешанных стратегиях (или функцией игры) или платежной функцией игры с матрицей, заданной табл. 4.
- Функцию М(Р, q) можно задать в матричной форме М(Р, q ) = РАqT, где Р = (р1, р2, …, рm) – вектор строка размера [1´m],
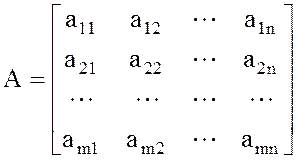 – матрица выигрышей игрока А в чистых стратегиях
(матрица размер [m´n]),
– матрица выигрышей игрока А в чистых стратегиях
(матрица размер [m´n]),
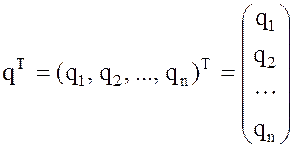 –
вектор столбец размер [n ´1].
–
вектор столбец размер [n ´1].
Проигрыш игрока В в
ситуации (Ak,q) определяется
по формуле
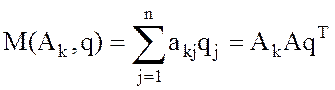 .
.
- Выигрыш игрока А в ситуации (р, Вk) определяется по формуле
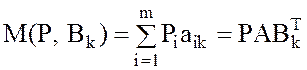 .
.
- Для функции М (р, q) можно вывести и некоторые другие формулы:
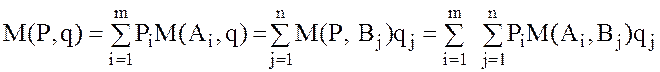 .
.
-
Показатель эффективности смешанной стратегии р игрока А относительно
множества `SB смешанных стратегий игрока В определяется по формуле 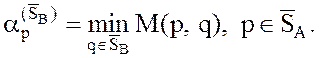
- Показатель эффективности смешанной стратегии р игрока А
относительно множества SB чистых стратегий
игрока В определяется по формуле 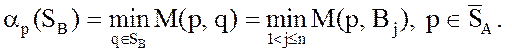
- Показатель неэффективности смешанной стратегии q игрока В относительно множества `SA смешанных стратегий игрока А
определяется по формуле 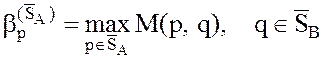 .
.
- Показатель
неэффективности смешанной стратегии q игрока В относительно множества SA чистых стратегий игрока А определяется по формуле
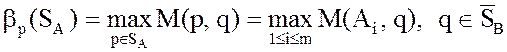 .
.
-
Нижней ценой (или максимином) матричной игры в смешанных стратегиях называется
величина 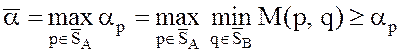 , где aр – показатель эффективности смешанной стратегии р игрока А.
, где aр – показатель эффективности смешанной стратегии р игрока А.
-
Верхней ценой (или минимаксом) матричной игры в смешанных стратегиях называется
величина 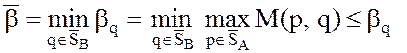 , где bq – показатель неэффективности смешанной
стратегии q игрока В.
, где bq – показатель неэффективности смешанной
стратегии q игрока В.
Теорема 2. Нижняя цена игры a и верхняя цена игры В в чистых стратегиях, нижняя цена игры `a и верхняя цена игры `b в смешанных стратегиях удовлетворяют следующим неравенствам a £`a £`b £ b.
11.6. Седловая точка в смешанных стратегиях
Если нижняя и верхняя цены игры в смешанных стратегиях совпадают, то их общее значение `g =`a =`b называется ценой игры в смешанных стратегиях, а стратегии p0 и q0, для которых выполняется равенство `g =`aр0 =`bq0 (и тогда это общее значение равно M(p0,q0), т.е. M(p0,q0) = `g ), называются оптимальными смешанными стратегиями соответственно игрока А и В.
Теорема 3. (Основная теорема матричных игр Фон Неймана).
Любая матричная игра имеет решение в смешанных стратегиях, т.е. существуют цена игры в смешанных стратегиях `g и оптимальные смешанные стратегии p0 и q0 соответственно игроков А и В, т.е.
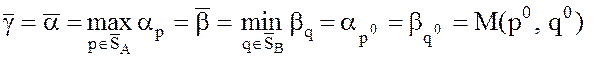 .
.
Теорема 4. Пусть `g – цена игры, М(р, q) – функция выигрыша, `SА,`SВ – множества смешанных стратегий соответственно игроков А и В.
1). Для того чтобы
стратегия p0 игрока А была
оптимальной, необходимо и достаточно, чтобы выполнялось неравенство 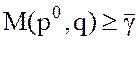 для любого
qÎ`SB, т.е. выбор игроком А оптимальной
стратегии p0 гарантирует ему выигрыш M(p0,q), не меньший цены игры`g при любой стратегии q
игрока В.
для любого
qÎ`SB, т.е. выбор игроком А оптимальной
стратегии p0 гарантирует ему выигрыш M(p0,q), не меньший цены игры`g при любой стратегии q
игрока В.
2). Для того чтобы
стратегия q0 игрока B была оптимальной, необходимо и достаточно, чтобы выполнялось
неравенство 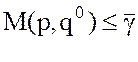 для любого рÎ`SА, т.е. выбор игроком В одной из
своих оптимальных стратегий q0 гарантирует ему проигрыш, не больший цены игры`g при любой стратегии р игрока А.
для любого рÎ`SА, т.е. выбор игроком В одной из
своих оптимальных стратегий q0 гарантирует ему проигрыш, не больший цены игры`g при любой стратегии р игрока А.
Теорема 5. Пусть `g – цена игры, M(p,q) – функция выигрыша, Ai и Bj, i = 1, 2, …, m, j = 1, 2, …, n – чистые стратегии соответственно игроков А и В.
1). Для того чтобы стратегия p0 игрока А была оптимальной, необходимо и достаточно, чтобы M(p0,Вj) ³`g , j = 1, 2, …, n.
2). Для того чтобы стратегия q0 игрока B была оптимальной, необходимо и достаточно, чтобы (Ai, q0) £`g, i = 1, 2, …, m.
Теорема 6. Для того чтобы `g была ценой игры, а p0 и q0 – оптимальными стратегиями соответственно игроков А и В, необходимо и достаточно выполнение двойного неравенства M(p, q0) £`g = M(p0,q0) £ М(p0,q) для любых рÎ`SА и qÎ`SB.
Теорема 7. Для того чтобы `g была ценой игры, а p0 и q0 – оптимальными стратегиями соответственно игроков А и В, необходимо и достаточно выполнение двойного неравенства M (Ai, q0) £`g = M (p0, q0) £ M (p0, Bj), i = 1, 2, …, m, j = 1, 2, …, n.
Пара смешанных стратегий (p0,q0) называется седловой точкой функции M(p, q), если M(p, q0) £ M(p0,q0) £ М(p0,q).
Т.е. если их применение обеспечивает игроку А средний выигрыш, не меньший, чем при применении им любой другой стратегии Р, игроку В – средний проигрыш, не больший, чем при применении им любой другой стратегии q.
Теорема 8. Для того чтобы `g была ценой игры, а p0 и q0 – оптимальными стратегиями соответственно игроков А и В, необходимо и достаточно, чтобы (p0,q0) была седловой точкой функции выигрыша M (p, q) и M (p0, q0) = `g.
11.7.Свойства оптимальных стратегий
Пусть![]() и
и ![]() –
оптимальные стратегии соответственно игроков А и В. В общем случае некоторые из
вероятностей
–
оптимальные стратегии соответственно игроков А и В. В общем случае некоторые из
вероятностей ![]() могут быть равными нулю.
могут быть равными нулю.
Если ![]() , где i – одно из
чисел 1, 2, …, m, то в оптимальной смешанной стратегии
, где i – одно из
чисел 1, 2, …, m, то в оптимальной смешанной стратегии ![]() чистая стратегия Ai не участвует и поэтому называется пассивной.
чистая стратегия Ai не участвует и поэтому называется пассивной.
Чистые стратегии Ai, входящие в оптимальную стратегию
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.