Основные понятия теории массового обслуживания на примерах

Глава 12. Теория массового обслуживания

12.1.Основные понятия

1. Система массового обслуживания (СМО) – это любая система, предназначенная для обслуживания каких-либо заявок (требований), поступающих в какие-то случайные моменты времени.

2. Канал обслуживания (прибор) – это любое устройство, непосредственно занимающееся обслуживанием заявок.

По числу каналов СМО делится на одноканальные и многоканальные.

3. Поток событий – это последовательность событий, наступающих одно за другим в какие-то, в общем случае, случайные моменты времени.

4. События в потоке называются однородными, если они различаются только по моментам их наступления.

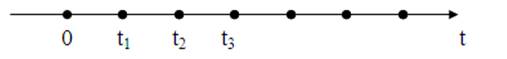
Рис. 1. Изображение однородных событий моментами их наступления

5. Поток событий называется:

a) регулярным, если события в нем наступают последовательно через строго определенные промежутки времени.

b) потоком без последствия, если для любой пары непересекающихся промежутков времени r₁ и r₂ число событий, наступающих за один из них, не зависит от числа событий, наступающих за другим.

Рис. 2. Изображение событий, наступающих в непересекающиеся промежутки времени r₁ и r₂

На рис. 2 r₁ и r₂ – длина временных непересекающихся промежутков;

c) ординарным, если вероятностью наступления за элементарный (малый) промежуток времени Dt более одного события можно пренебречь по сравнению с вероятностью наступления за этот промежуток не более одного события.

Ординарность потока означает, что события в нем за достаточно малый промежуток времени либо не наступают, либо наступают по одному, а не по несколько;

d) стационарным, если вероятность наступления того или иного числа событий за какой-либо промежуток времени зависит только от длины этого промежутка и не зависит от момента его начала.

Стационарность потока означает, что его вероятностные характеристики не зависят от времени;

e) пуассоновским, если он ординарный без последствия;

f) простейшим, если он стационарный пуассоновский.

6. Интенсивность потока событий l (средняя плотность потока) – это среднее число событий потока, наступающих в единицу времени.

-Интенсивность простейшего потока не меняется с течением времени l = const.

-Интенсивность пуассоновского потока зависит от времени t l= l(t).

7.Теорема. Пусть Х(r) – случайная дискретная величина, предоставляющая собой число событий, наступающих за промежуток времени r.

Таким образом, случайная величина Х(r) может принимать значение m=0,1,2,… .

Пусть  - вероятность того, что за промежуток времени r в потоке наступит только m событий.

В простейшем потоке с интенсивностью l = const случайное число событий Х(r), наступающих за промежуток времени r, распределено по закону Пуассона

.

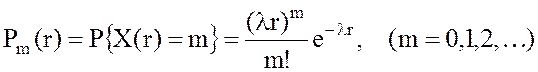Его математическое ожидание (т.е. среднее число событий, наступающих в потоке за промежуток времени r)  и дисперсия D[X(r)] равны , а среднее квадратическое отклонение . Таким образом:

-вероятность того, что за промежуток времени r не наступит ни одного события, (Х(r) = 0, т.е. участок r окажется свободным):

;

-вероятность того, что за промежуток времени r в потоке наступит менее k (k = 1,2,3,…) событий (X(r)<k):

;

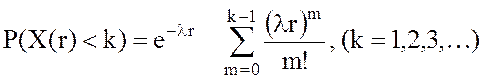-вероятность того, что за промежуток времени r в потоке наступит не менее k (k = 1,2,3,…) событий (X(r)³k):

;

-вероятность того, что за промежуток времени r в потоке наступит хотя бы одно событие (X(r)³1, т.е. временной участок r окажется занятым):

;

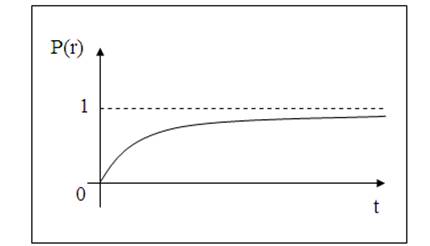
Рис. 3

-интенсивность потока l равна .

8.Теорема. Пусть Т – непрерывная случайная величина, представ ляющая собой промежуток времени между двумя любыми соседними событиями потока: 0 < T < ∞.

Пусть P(T < t), (t ³ 0) – вероятность того, что промежуток времени Т между двумя любыми соседними событиями меньше t, (t³0). В простейшем потоке с интенсивностью l = const для случайной величины Т:

a) интегральная функция распределения

.

Следовательно, вероятность Р(Т³t) того, что промежуток времени Т между двумя любыми соседними событиями будет меньше t:

, где события (T < t) и (T ³ t) противоположны.

На рис. 4 величина вероятности того, что значение промежутка времени Т между двумя соседними событиями в потоке окажется в интервале (0,а), равна y;

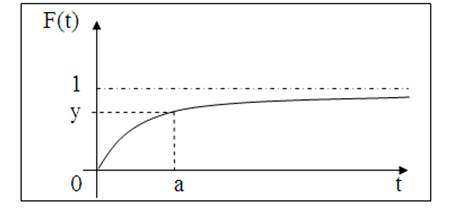
Рис. 4. График интегральной функции распределения F(t)

b) дифференциальная функция распределения (или плотность распределения) ,

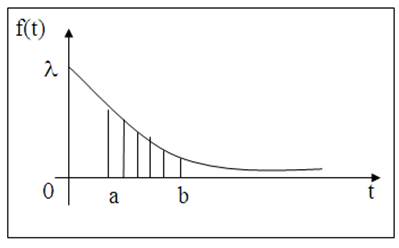
Рис. 5. График дифференциальной функции распределения f(t)

т.е. Т имеет показательное (экспоненциальное) распределение с параметром l. На рис. 5 величина вероятности того, что значение промежутка времени Т между двумя соседними событиями в потоке окажется в ин тервале (а,b) равна площади кривой под трапецией aABb;

c) математическое ожидание (средний интервал времени между двумя соседними событиями) ;

d) дисперсия  ;

e) среднее квадратическое отклонение.

9. Вероятности состояний системы в предельном стационарном режиме (не зависят ни от времени, ни от начального распределения) называются предельными (финальными или стационарными) вероятностями, т.е. финальные вероятности не зависят от времени t в стационарном режиме.