Таким образом, непрерывная случайная величина Тоб[4] (время обслуживания одним каналом одной заявки) распределена по показательному закону с параметром m = const. Функция распределения
![]() (t ³ 0), плотность
распределения [5]
(t ³ 0), плотность
распределения [5]![]() (t ³ 0), математическое
ожидание (среднее время обслуживания одной заявки одним каналом)
(t ³ 0), математическое
ожидание (среднее время обслуживания одной заявки одним каналом) ![]()
дисперсия ![]() , среднее
квадратическое отклонение
, среднее
квадратическое отклонение ![]() .
.
4. Рассмотрим интервал времени, когда канал не занят обслуживанием. Поскольку интервалы простоя обслуживающего канала начинается с моментов завершения обслуживания и заканчивается при поступлении нового требования, продолжительность простоя каналов имеет такое же распределение, как и длительность интервалов между поступлениями требований, т.е. показательное распределение с параметром l = const.
Средняя длина интервала (математическое
ожидание) равна ![]() .
.
5. В начальный момент времени t = 0 канал свободен, первое поступление имеет место в момент t (t>0). Требуется:
1. Построить граф состояния СМО. 2. Определить показатели СМО.
Решение.1. Состояние системы занумеруем по числу заявок, находящихся в системе
s0 – канал свободен (ожидание),
s1 – канал занят (идет обслуживание заявки).
Граф состояний показан на рис. 8
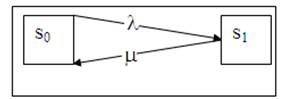
Рис. 8
2. Показатель нагрузки СМО (величина является безразмерной).
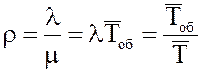 эрланг[6],
(0<r<∞), где
эрланг[6],
(0<r<∞), где 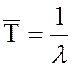 - средний интервал времени между двумя
соседними заявками во входящем потоке (средняя длительность промежутков времени
между последовательными моментами прибытия клиентов).
- средний интервал времени между двумя
соседними заявками во входящем потоке (средняя длительность промежутков времени
между последовательными моментами прибытия клиентов). ![]() .
.
3. Финальные вероятности состояний СМО.
Вероятность того, что канал свободен
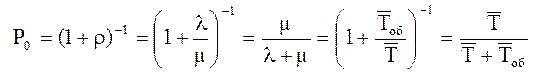 . (1)
. (1)
Обозначаем через
Р(k;ρ) = ![]() , k=0,1,2,…. (2)
, k=0,1,2,…. (2)
Тогда
Р(0,ρ) = ![]() =1,Р(1,ρ) =
=1,Р(1,ρ) = ![]() =ρ,Р(2,ρ) =
=ρ,Р(2,ρ) = ![]() , и т. д.
, и т. д.
Обозначаем через
R(m;ρ) = 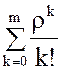 , k=0,1,2,…. (3)
, k=0,1,2,…. (3)
Тогда R(0;ρ) = 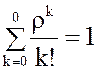 ,R(1;ρ) =
,R(1;ρ) = 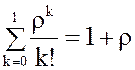 , и т.д., где Р(k;ρ) и R(m;ρ) – табличные функции распределения Пуассона.
, и т.д., где Р(k;ρ) и R(m;ρ) – табличные функции распределения Пуассона.
Таким образом, из (1) и (2) получим
Р0
= (1+ρ)-1 = 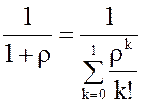 ,
,
Вероятность того, что канал занят:
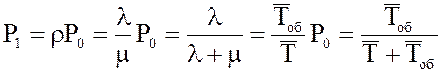 . (4)
. (4)
Из (2),(3) и (4) получим
Р1
= ρ Р0 = ![]() =
= 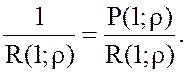
4. Вероятность отказа равна вероятности того, что канал СМО занят, т.е. вероятности того, что СМО находится в состоянии s1:
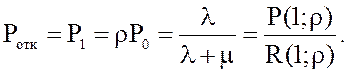
5.
Так как событие, состоящее в том, что пришедшая заявка получит отказ, и событие
принятия пришедшей заявки на обслуживание являются противоположными, то сумма
их вероятностей равна 1, т.е. Ротк + Роб=1. Таким образом, вероятность того, что пришедшая
заявка будет обслужена: Роб = 1 - Ротк = 1 - Р1
= 1 - r×Р0 = 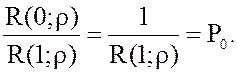
6.
Относительная пропускная способность равна вероятности обслуживания заявки 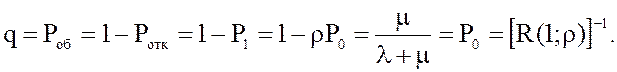
7. Абсолютная пропускная способность или среднее число заявок, которое может обслужить СМО за единицу времени:
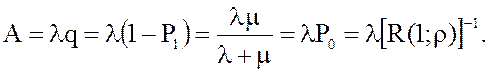
8. Интенсивность выходящего потока обслуженных заявок (который, подчеркнем, не следует путать с потоком обслуживания)
![]()
9. Среднее число
занятых каналов можно подсчитать следующим образом: так как абсолютная
пропускная способность А есть среднее число заявок, обслуживаемых СМО в единицу
времени, а один занятый канал обслуживает в среднем за ту же единицу времени m заявок, то среднее
число занятых каналов ![]() будет равно
будет равно
[7]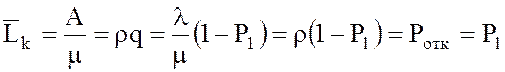 .
.
Можно подсчитать величину ![]() как математическое ожидание M[K] дискретной случайной величины К,
представляющей собой число занятых каналов, которая может принимать значения 0
и 1 с вероятностью соответственно Р0, Р1.Тогда
как математическое ожидание M[K] дискретной случайной величины К,
представляющей собой число занятых каналов, которая может принимать значения 0
и 1 с вероятностью соответственно Р0, Р1.Тогда
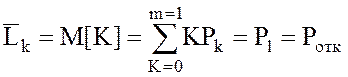 , где Р0 +
Р1 = 1, Р1 = r×Р0.
, где Р0 +
Р1 = 1, Р1 = r×Р0.
10.
Среднее число заявок под обслуживанием ![]() :
:
11.
Среднее число заявок, находящихся в СМО ![]() :
:
12. Среднее время пребывания заявки в СМО
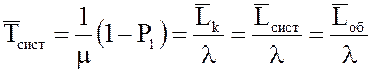 =(μ R(1;ρ))-1.
=(μ R(1;ρ))-1.
13. Среднее время
обслуживания заявки, относящееся ко всем заявкам - как обслуженным, так и
получившим отказ: ![]() .
.
Среднее
время ![]() не следует путать со средним временем
обслуживания заявки
не следует путать со средним временем
обслуживания заявки 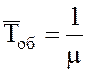 , которое относится только к
обслуженным заявкам.
, которое относится только к
обслуженным заявкам.
14.
Вероятность того, что канал (любой) занят: Рз.к. = 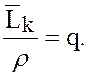
15. Вероятность того, что система полностью загружена:
Рп.з.
= Ротк = Р1 = 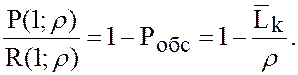
16.
Среднее время занятости канала 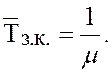
17.
Среднее время простоя канала 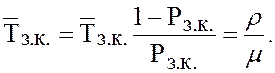
18.
Среднее время полной загрузки системы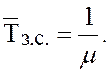
19. Среднее время неполной загрузки системы 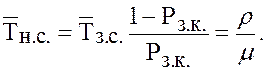
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.