Математика \ Математическое программирование

Основные понятия теории массового обслуживания на примерах, страница 12

-  Заявка, поступавшая в момент, когда все m каналов заняты, становится в очередь и ожидает обслуживания.

- Любая пришедшая заявка будет обслужена. Требуется:

1. Построить граф состояний СМО.

2. Найти показатели эффективности СМО.

3. Определить вероятность того, что обслуживания ожидает не более ν заявок, v>m.

Решение.1. Состояния СМО нумеруются по числу заявок, находящихся в очереди или обслуживаемых:

s0 – СМО свободна (все каналы свободны);

s1 – канал занят, остальные свободны;

s2 – два канала заняты, остальные свободны;

………………………………………………………………………………

sk – занято k каналов, остальные свободны;

………………………………………………………………………………

sm – заняты  все m каналов (очереди нет);

sm+1 – заняты все m каналов, одна заявка стоит в очереди;

………………………………………………………………………………

sm+n – заняты все mканалов, n заявок стоит в очереди;

………………………………………………………………………………

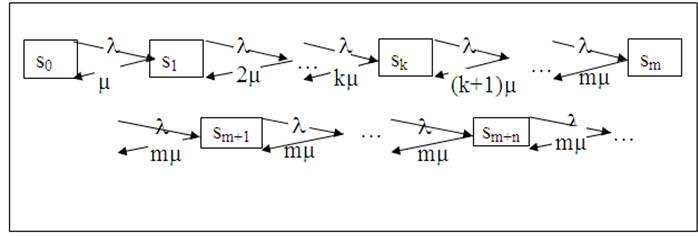
Рис. 14

2. Показатель нагрузки СМО. Доказано, что если а) 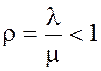, то вероятности состояний СМО существуют.

b) 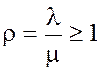, то очередь растет до бесконечности.

3. Показатель (коэффициент) нагрузки, приходящийся на один канал

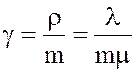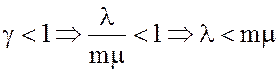,  (вероятности состояний СМО существуют); (очередь заявок в системе с течением времени будет неограниченно расти).

4. Вероятность того, что СМО свободна:

.

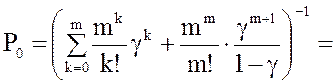
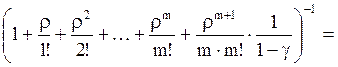
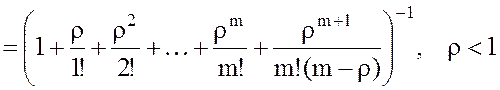5. Вероятность любого состояния sk СМО, k=1,2,…

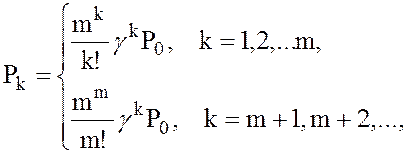 или

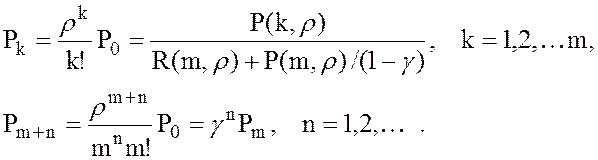
6. Вероятность отказа заявке Ротк = 0.

7. Вероятность того, что заявка будет принята в СМО: Рсист = 1- Ротк = 1.

8. Относительная пропускная способность q = Рсист = 1- Ротк = 1.

9. Вероятность того, что заявка окажется в очереди  .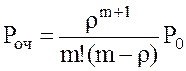

10. Абсолютная пропускная способность A = λ∙q = λ∙1 = λ.

11. Среднее число занятых каналов 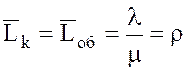, ρ < m.

12. Среднее число заявок, находящихся в очереди:

.

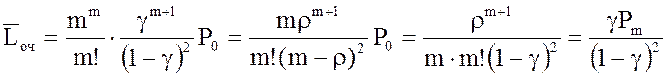13. Среднее число заявок, находящихся в СМО (как в очереди, так и под обслуживанием):

.

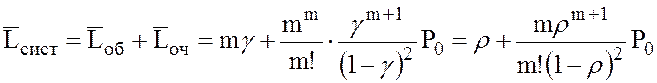14. Среднее время ожидания заявки в очереди

.

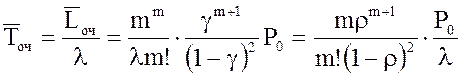15. Среднее время пребывания заявки в системе

.

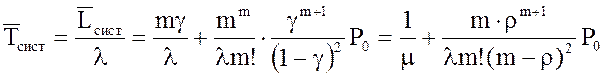16. Среднее время обслуживания одной заявки

.

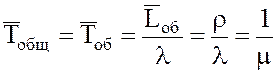17. Вероятность того, что обслуживание ожидает не более ν заявок, ν>m, т.е. в очереди будет не более ν заявок:

.или

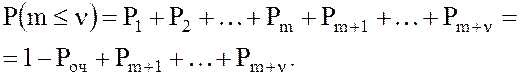
18. Вероятность того, что система полностью загружена:

.

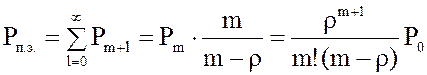19. Вероятность того, что канал занят: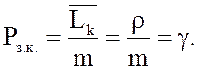

20. Среднее время неполной загрузки системы .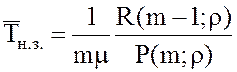

21. Среднее время полной загрузки системы .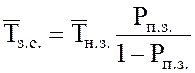

22. Вероятность наличия очереди в системе

.

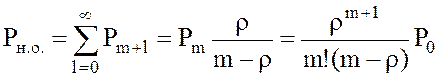23. Среднее время наличия очереди .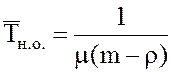

24. Среднее время занятости канала .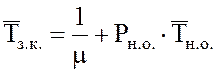

25. Среднее время простоя канала .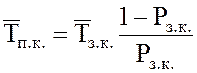

Пример 9. - В билетной кассе автовокзала имеется одно окно.

- Кассир тратит на обслуживание пассажира в среднем  мин.

- Среднее число пассажиров, желающих приобрести билеты в кассе, в течение одной минуты равно l=3 пас./мин.


[1] - интенсивность поступления заявок l выражает скорость поступления заявок на обслуживание (средняя плотность потока). l=const, т.е. l не зависит от времени t;

- интенсивность простейшего входящего потока заявок;

- число входящих заявок в единицу времени.

[2] Т – длительность интервалов между поступлениями заявок.

[3] Интенсивность простейшего «потока обслуживания», или интенсивность обслуживания m, характеризует скорость работы канала обслуживания (средняя продолжительность обслуживания). Интенсивность потока обслуживания m есть ни что иное, как производительность канала.

[4] Тоб – время, в течение которого какая-либо заявка находится на обслуживании, называется длительностью обслуживания.

[5] g(t) – плотность распределения вероятностей того, что в интервале, продолжительность которого равняется t, будет обслужена одна заявка (t ≥ 0).

[6] Эрланг – единица измерения показателя r.

7  – интенсивность потока обслуженных СМО заявок в единицу времени.

[8]Pk - при больших значениях m вероятности состояний СМО Pk удобно вычислять через табулирование функции:

  распределение Пуассона,                                                                                                                 (1)

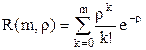                                                                                                                                                            (2)

, из которых (1) можно выразить через (2), а именно , где

Скачать файл