Основные понятия теории массового обслуживания на примерах, страница 5

20. Среднее время простоя системы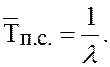

Пример 2. - Одноканальная СМО с отказами представляет собой один пост ежедневного обслуживания (ЕО) для мойки автомобилей.

- Заявка – автомобиль, прибывший в момент, когда пост занят, или в последний момент рабочего дня, получает отказ в обслуживании.

- В потоке автомобилей интервал времени между соседними поступающими автомобилями – величина случайная. Автомобили поочередно поступают к посту в момент времени: 8:00, 8:30, 9:40, 10:02, 11:20, 11:56, 13:42, 14:40, 15:55, 16:30, 18:00. Интервал между поступлениями равен: 30, 70, 22, 78, 36, 106, 58, 75, 35, 90 минут.

- Пост (ЕО) затратил на обслуживание каждого из пяти первых автомобилей различное время: 110, 100, 95, 120, 115 минут.

- Поток автомобилей (заявок) и поток обслуживаний являются простейшими. Требуется:

1. Определить показатели СМО,

2. Построить граф состояния,

3. Сравнить фактическую пропускную способность СМО с номинальной, которая была бы, если бы каждый автомобиль обслуживался точно 1,8 часа и автомобили следовали бы один за другим без перерыва.

Решение. Рассмотрим на оси 0t (час) поток заявок (автомобилей) для обслуживания.

    - означает, что заявка принята к обслуживанию.

    - означает, что заявка получает отказ.

Пусть какая-то заявка ▄, пришедшая в момент t₁, принята к обслуживанию. Тогда все заявки , пришедшие после нее за время , получат отказ. Следующей будет принята к обслуживанию заявка ▄, пришедшая в момент t₂ такой, что t₂ – t₁ >  (см. рис. 9) или , где  - интервал между концом обслуживания первой заявки и моментом t₂ прихода ближайшей следующей, которая будет принята к обслуживанию.

Рассчитаем величины.

1. Средняя длительность промежутков времени между последовательными моментами прибытия автомобилей

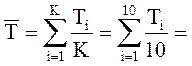
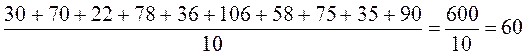 мин.

2. Интенсивность поступления заказов (среднее число поступающих в единицу времени)

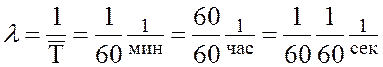, т.е. за одну секунду на обслуживание в среднем прибывает 1/3600 автомобиля, за одну минуту – 1/60 автомобиля, за один час – 1 автомобиль.

3. Среднее время обслуживания одного автомобиля одним каналом

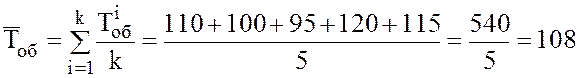 мин.

4. Интенсивность обслуживания (среднее число автомобилей, обслуживаемое одним каналом за единицу времени)

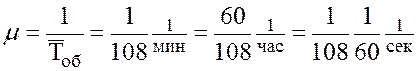,т.е. за 1 секунду пост (ЕО) обслуживает в среднем 1/108 60, за 1 минуту – 1/108 и за 1 час – 60/108≈1/1,8 автомобиля.

5. Среднее число заявок за среднее время обслуживания (показать нагрузки системы)

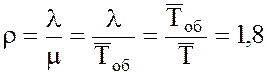 эрланг.

6. Вероятность того, что канал свободен: Р₀ = (1 + ρ)^-1 = (1+1,8)^-1 ≈ 0,356.

7. Вероятность того, что канал занят: Р₁ = ρ Р₀ = 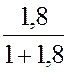 ≈ 0,644.

8. Вероятность отказа .

Это означает, что около 65% автомобилей, прибывших на пост (ЕО), получают отказ в обслуживании.

9. Вероятность обслуживания (с вероятностью того, что пришедший автомобиль будет обслужен) .

10. Относительная пропускная способность .

Это означает, что в установившемся режиме система будет обслуживать примерно 35% прибывающих автомобилей.

11. Абсолютная пропускная способность , т.е. система способна осуществить обслуживание в среднем 0,356 автомобиля в час.

12. Интенсивность выходящего потока обслуженных автомобилей

.

13. Среднее число занятых каналов  .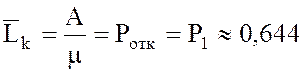

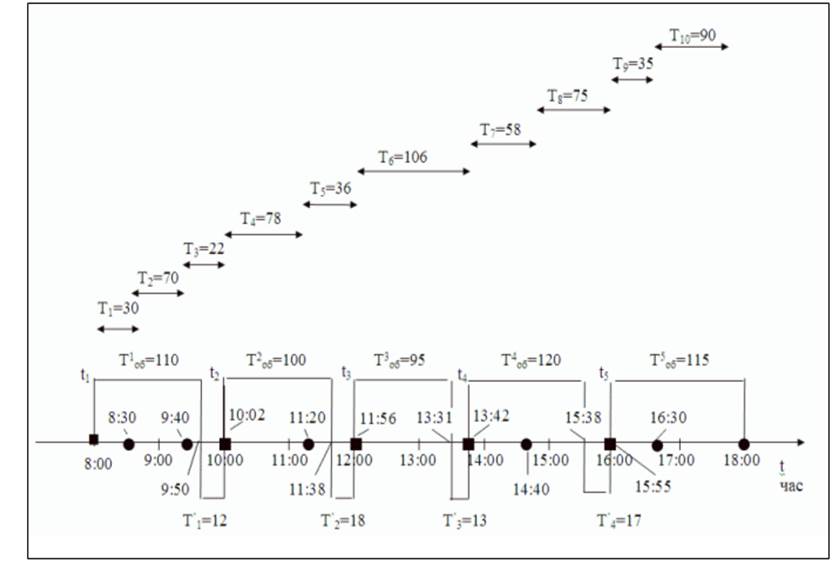
Рис. 9

Примечание:  Тⁱ_об и Т_i – задаются в минутах.

14. Среднее число заявок (автомобилей) под обслуживанием .

15. Среднее число заявок (автомобилей) в СМО  .

16. Среднее время пребывания заявки (автомобилей) в СМО

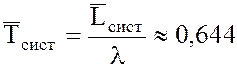 час.

17. Среднее время облуживания заявки (автомобилей), относящееся ко всем заявкам (автомобилям) – как к обслуженным, так и к получившим отказ: час.

18. Граф состояния

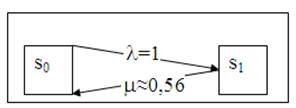
Рис. 10

19. Среднее время простоя канала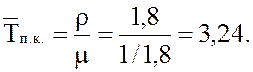  

20. Номинальная пропускная способность канала была бы (при регулярно проходящих и регулярно обслуживаемых заявках)

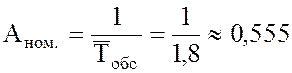 (автомобиля/час).

Но А_ном в 1,5 раза больше, чем фактическая пропускная способность, вычисленная с учетом случайного характера потока заявок и времени обслуживания .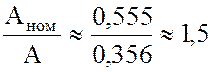

Решение задачи СМО на ЭВМ с использованием программы Excel

По условию задачи m=1, λ=1, μ=

1.  Щелкнем ПКМ по активной ячейке (например А₁),открываем контекстное меню.