Основные понятия теории массового обслуживания на примерах, страница 11

16. Вероятность того, что обслуживание ожидает не более ν заявок, т.е. в очереди будет не более ν заявок: .

17. Вероятность того, что система полностью загружена: Р_п.з.= ρ².

18. Среднее время неполной загрузки системы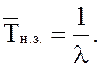

19. Среднее время полной загрузки системы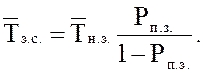

20. Среднее время наличия очереди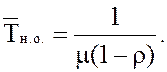

21. Вероятность наличия очереди в системе Р_н.о.= ρ².

22. Среднее время занятости канала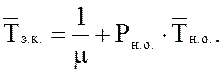

23. Среднее время простоя канала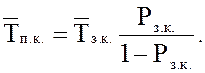

Пример 7.- Железнодорожная сортировочная станция (ЖСС), на которую поступает простейший поток составов с интенсивностью λ = 0,85 состава/час, представляет собой одноканальную СМО с неограниченной очередью.

- Обслуживание (расформирование) состава длится случайное (показательное) время с₀ со средним значением  час. Требуется:

1. Найти показатели эффективности СМО.

2. Построить граф состояний системы.

3. Определить вероятность того, что обслуживания ожидает не более 4 -х составов.

Решение.1. Интенсивность простейшего потока обслуживания или среднее число составов, обслуживаемых одним каналом за час при непрерывной его работе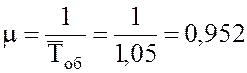 составов/час.

2. Показатель нагрузки СМО .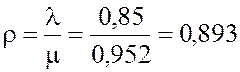

3. Вероятность того, что система ЖСС свободна: Р₀ = 1 – ρ = 1 - 0,893 = 0,107.

4. Вероятность любого состояния s_k СМО k = 1,2,…

Р₁ = (1 – ρ)∙ρ = (1-0,893)∙0,893 = 0,096;

Р₂ = (1 – ρ)∙ρ² = (1-0,893)∙0,893² = 0,085;

Р₃ = (1 – ρ)∙ρ³ = (1-0,893)∙0,893³ = 0,076;

Р₄ = (1 – ρ)∙ρ⁴ = (1-0,893)∙0,893⁴ = 0,068;

Р₅ = (1 – ρ)∙ρ⁵ = (1-0,893)∙0,893⁵ = 0,061 и т.д.

5. Вероятность того, что канал занят: Р_з.к. = 1 – Р₀ = ρ = 0,893.

6. Вероятность отказа в обслуживании состава Р_отк = 0.

7. Вероятность того, что пришедший состав будет принят в систему ЖСС: Р_сист = 1 – Р_отк = 1.

8. Относительная пропускная способность q = Р_сист = 1 – Р_отк = 1.

9. Абсолютная пропускная способность

A = λ∙q = λ∙1 = λ = 0,85 состава/час.

10. Среднее число составов, находящихся под обслуживанием:

.

11. Среднее число составов, ожидающих очереди на расформирование (все равно, на каких путях): .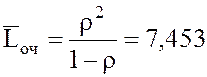

12. Среднее число составов, связанных со станцией:

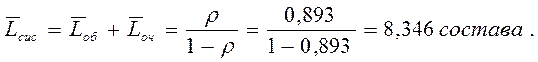
13. Среднее время пребывания составов на очереди

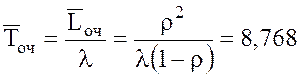 час.

14. Среднее время (продолжительность) пребывания состава при станции (на внутренних, внешних путях и под обслуживанием)

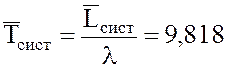 час.

15. Среднее время обслуживания одного состава

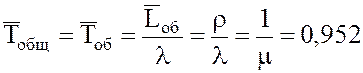 час.

16. Среднее время неполной загрузки системы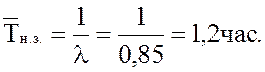

17. Вероятность того, что система полностью загружена:

Р_п.з. = ρ² = (о,893)² = 0,8.

18. Среднее время полной загрузки системы

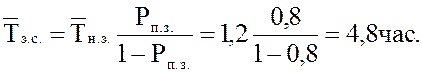
19. Среднее время наличия очереди

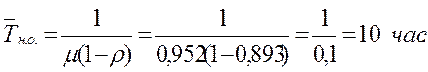
20. Вероятность наличия очереди в системе Р_н.о. = ρ² =0,8.

21. Среднее время занятости канала

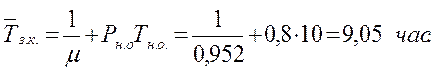
22. Среднее время простоя канала

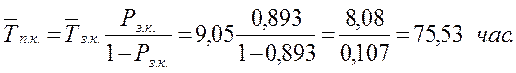
23. Граф состояния

Рис. 13

24. Вероятность того, что обслуживания ожидает не более 4 - х составов:

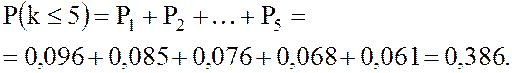
Пример 8. - Система массового обслуживания - билетная касса с одним окошком (m=1) и неограниченной очередью.

- Касса продает билеты в пунктах X и Y.

- Пассажиров, желающих купить билет в пункт Х, приходит в среднем трое за 20 мин., в пункт Y – двое.

- Поток пассажиров можно считать простейшим.

- Кассир в среднем обслуживает трех пассажиров за 10 мин.

- Время обслуживания распределяется по показательному закону, т.е. поток обслуживания простейший. Требуется:

Найти показатели эффективности СМО.

Решение.1. Среднее число пассажиров, желающих купить билет в пункт Х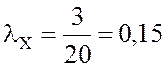 заявки/мин.

2. Среднее число пассажиров, желающих купить билет в пункт У

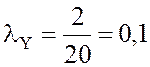 заявки/мин.

3. Общая интенсивность потока заявок  заявки/мин.

4. Интенсивность потока обслуживания 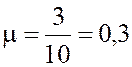 заявки/мин.

5. Показатель нагрузки системы , это означает, что вероятности состояния системы существуют.

6. Р₀ = 1 – ρ = 1-0,833=0,167.

7.  и т.д.

8. Вероятность того, что канал занят: Р_з.к. = 1 –Р₀ = ρ = 0,833,

9. Р_отк = 0.

10. Р_сист = 1 –Р_отк = 1.

11. q = P_сист = 1.

12. A = λ∙q = 1∙0,25 = 0,25.

13. .

14. 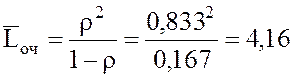 заявки.

15.  заявки.

16. 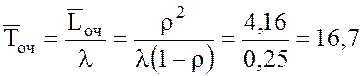 мин.

17. 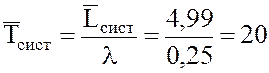 мин.

12.5.Многоканальная СМО с неограниченной очередью

- На m-канальную СМО поступает простейший поток заявок с интенсивностью λ = const.

- Поток обслуживаний также простейший с интенсивностью μ=const>0.