Математика \ Математическое программирование

Основные понятия теории массового обслуживания на примерах, страница 6

2.   Щелкнем ЛКМ по строке «формат ячейки» и выберем «число» → «числовые форматы»: «дробный» → «тип»: дробями до трех цифр () → «Ок».

Замечания.1º. Командами «формат ячеек» → «выравнивание» → «по горизонтали» (по центру) провести выравнивание элементов любых столбцов А,В,С,D… по центру.

2º. Можно изменить ширину столбцов: устанавливаем курсор мыши в форме знака (+) на правой или левой стороне столбца и, когда появится двусторонняя стрелка, щелкнем ЛКМ, но кнопку не отпускаем, а перемещаем границу, двигая мышью.

Аналогичным образом изменяем высоту строки.

3.  В диапазоне В1:В3 вводим условие задачи.

4.  В ячейку В4 вводим формулу: =В2/В3.

5.  В ячейки D1:D2 вводим формулы: = В4^0,  = B4^1.

6.  В ячейку D3 вводим формулу: = СУММ (D1:D2).

(Выделяется диапазон D1:D2, и с помощью кнопки находится сумма его (диапазона) элементов, автоматически записывается в D3).

7.  Введем в ячейку F1 формулу: =1/ D3 и находим Р0.

8.  Введем в ячейку F2 формулу: = В4* F1 и находим Р1 и Ротк (значение Ротк находится в ячейке F3).

9.  Введем в ячейку Н1 формулу: = 1- F3 и находим q.

10.  Введем в ячейку Н2 формулу: = В2* Н1 и находим А.

11.  Введем в ячейку Н3 формулу: = Н2/В3 и находим.

12.  Введем в ячейку Н4 формулу: = Н3/В2 и находим.

13.  Введем в ячейку Н5 формулу: = B4/В3 и находим.

А

В

С

D

E

F

G

H

1

m

1

1

P0

1/2,8

q

1/1,8

2

λ

1

1,8

P1

1,8/2,8

A

1/1,8

3

μ

1/1,8

P0^-1

2,8

Pотк

1,8/2,8

1,8/2,8

4

ρ

1,8

1,8/2,8

5

1,8/1/1,8

12.3.Многоканальная СМО с отказами

Постановка задачи

1.  На m-канальную СМО поступает простейший поток заявок на обслуживание (входящий поток) с интенсивностью l = const.

2.  Заявка, поступавшая на вход в момент, когда все m каналов заняты обслуживанием, получает отказ и покидает систему.

3.  Поток обслуживаний (выходящий поток) каждым каналом является простейшим с интенсивностью m = const > 0. Требуется:

1.  Построить граф состояния СМО.

2.  Определить показатели СМО.

Решение .1. Состояние системы будем нумеровать по числу заявок, находящихся в системе (в данном случае оно совпадает с числом за нятых каналов):

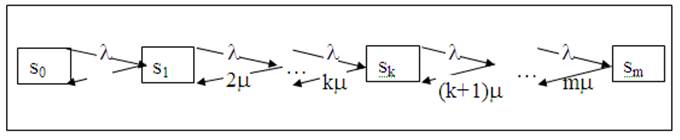
Рис. 11

s0 – СМО свободна, нет ни одной заявки, все m каналов свободны,

s1 – в СМО находится одна заявка, один канал занят, остальные m-1 каналов свободны;

………………………………………………………………………………

sk – в СМО находится k заявок, k каналов занято, остальные m-k каналов свободны;

………………………………………………………………………………

sm – в СМО находится m заявок, все m каналов заняты.

2. Проставим у верхних стрелок интенсивность потоков событий. Поток заявок последовательно переводит систему из любого левого состояния в соседнее правое с одной и той же интенсивностью l.

3. Проставим интенсивность у нижних стрелок. Пусть система находится в состоянии s1 (работает один канал). Он производит m обслуживаний в единицу времени. Проставляем у стрелки s1® s0 интенсивность m. Если СМО находится в состоянии s2 (работают два канала), то она может перейти в состояние s1 (работает один канал), когда закончит обслуживание либо первый, либо второй канал, т.е. суммарная интенсивность их потоков обслуживаний будет равна 2m. Проставляем у стрелки s2® s1 интенсивность 2μ.Аналогично суммарный поток обслуживаний, переводящий СМО из состояния s3 (работают три канала) в s2, будет иметь интенсивность 3m, т.е. может освободиться один из трех каналов, и т.д.

Скачать файл