Это означает, что примерно в 57% случаев невозможно сделать заказ, так как телефон занят.
7. Вероятность того, что пришедшая заявка будет обслужена:
Роб = 1 - Ротк = 1 - Р1 = Р0 =3/7 ≈ 0,43.
Это означает, что примерно 43% времени стол заказов бездействует и лишь примерно 57% времени он занят оформлением заказов.
8. Относительная пропускная способность q = Роб ≈ 0,43.
9. Абсолютная пропускная способность A = λ∙q ≈ 1/3∙0,43 = 1,433.
10. Интенсивность выходящего потока обслуженных заявок V = A ≈ 14,33.
11.
Среднее число занятых каналов 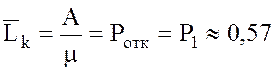 .
.
12.
Среднее число заявок под обслуживанием ![]() .
.
13.
Среднее число заявок, находящихся в СМО ![]() .
.
14.
Среднее время пребывания заявок в СМО 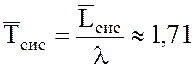 мин.
мин.
15. Среднее время обслуживания заявки, относящееся ко всем заявкам – как к обслуженным, так и к получившим отказ: ![]() мин.
мин.
Подключается второй телефон (m=2).
1.
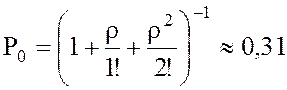 .
.
Это означает, что стол заказов бездействует 31% времени.
2. 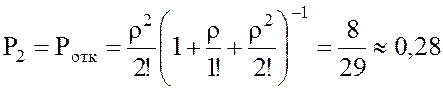 . Следовательно, оба телефона оказываются
занятыми и заказ сделать невозможно в 28% случаев.
. Следовательно, оба телефона оказываются
занятыми и заказ сделать невозможно в 28% случаев.
3. Среднее число занятых каналов 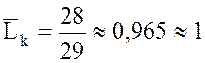 . Отсюда видно, что лишь один из двух
приемщиков занят оформлением заказов, а второй бездействует.
. Отсюда видно, что лишь один из двух
приемщиков занят оформлением заказов, а второй бездействует.
Пример 5. - В вычислительном центре работает m=2 персональных компьютеров (ПК).
- Простейший поток задач, поступающих в вычислительный центр (ВЦ), имеет интенсивность λ = 4 задач/час.
- Среднее время
решения задачи равно ![]() часа.
часа.
- Заявка получает отказ, если все ПК заняты.
- Каждое решение задачи приносит доход D = 4 (д.е.).
- Содержание каждого ПК обходится С = 2 (д.е.) в час.
- Определить: выгодно или нет в экономическом отношении увеличение числа ПК до трех?
- Определить число персональных компьютеров в ВЦ, для которого относительная пропускная способность системы будет не менее 0,8, т.е. q≥0,8.
Решение. 1. Находим вероятность того, что в ВЦ нет ни одной заявки
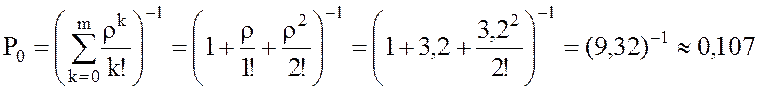 , где
, где ![]() .
.
2. Находим вероятность того, что в ВЦ заняты все m=2 ПК:
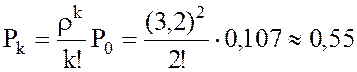 .
.
3. Находим относительную пропускную способность: q = 1 - P2 = 1 – 0,55 ≈ 0,45.
4. Находим абсолютную пропускную способность, т.е. среднее число заявок, которое сможет обслужить ВЦ в час: ![]() задач/час.
задач/час.
5. Находим доход от заявок, приносимый СМО в данном варианте:
D1 = D∙A ≈ 4∙1,8 ≈ 7,2 (д.е.)/час.
Подсчитаем те же показатели для трех ПК:
6. 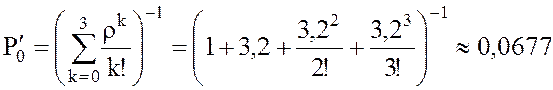 .
.
7. 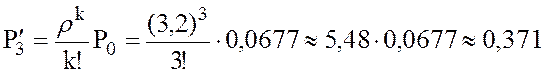 .
.
8. q′ = 1-P′3 = 1 – 0,371 ≈ 0,629.
9. ![]() .
.
10. D2 = D∙A′ ≈ 4∙2,52 ≈ 10,08 (д.е.)/час. Увеличение дохода равно
D* = D2 - D1 = 10,08 – 7,2 = 2,88 (д.е.)/час; увеличение расхода равно 2 (д.е.)/час. Из этого видно, что переход от m = 2 к m = 3 экономически выгоден.
Таблица 1
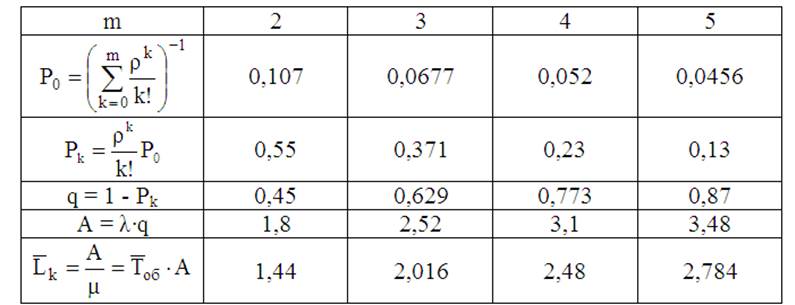
11. Для ВЦ определяем оптимальное число ПК, если условием оптимальности считать обслуживание в среднем не менее 9 задач. Число каналов (ПК) будем постепенно увеличивать m=3,4,5,…. Результаты расчета характеристик для получаемой m-канальной СМО представлены в табл. 1.
Условие задачи q ≥ 0,8 удовлетворяется для пяти ПК, при этом q=0,87.
В час будет обслуживаться в среднем А = 3,48 заявки. Среднее число занятых ПК ![]() . Вероятность отказа Ротк = Р5
= 0,13.
. Вероятность отказа Ротк = Р5
= 0,13.
Пример 6. - Имеется простейшая трехканальная СМО с отказами. На нее поступает поток заявок с интенсивностью λ = 20 (заявок/час).
- Среднее время обслуживания заявки одним каналом 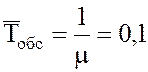 час.
час.
- Обслуживание одной
заявки приносит средний доход ![]() д.е.
д.е.
-
Создание одного канала обслуживания требует средних издержек ![]() д.е.
д.е.
-
Эксплуатация одного канала в час требует средних издержек ![]() д.е. Требуется:
д.е. Требуется:
1. Найти показатели эффективности СМО .
2. Построить граф состояния СМО.
3. Найти среднее число заявок, обслуживаемых за время t.
4. Найти средний доход, который принесет система за время ее эксплуатации t.
5. Найти средний расход за время t.
6. Определить время t, через которое система начнет приносить прибыль.
7. Определить прибыль, даваемую системой через t1 = 300 час.
Решение.1. Показатель нагрузки СМО ![]() эрланга.
эрланга.
2. Вычисление вероятностей состояний СМО сведено в табл. 2.
Таблица 2
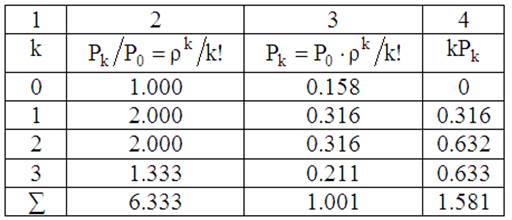
2.1. Производим вычисления во втором столбце по формуле
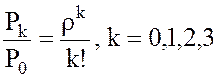 , которая следует из формулы
, которая следует из формулы 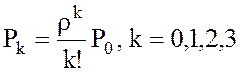
(k – число занятых каналов).
2.2.
Сумма всех элементов столбца (2)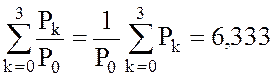 , отсюда
, отсюда
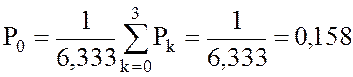 , где
, где 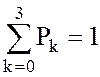 .
.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.