4. Дискретная случайная величина Х(r) – случайное число заявок, поступающих за промежуток времени r, распределено по закону Пуассона
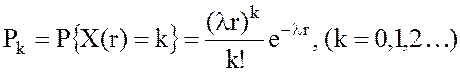 ;
;
его математическое ожидание (т.е. среднее число заявок, наступающих в потоке за промежуток времени r) и дисперсия равны:
![]() , а среднее
квадратическое отклонение
, а среднее
квадратическое отклонение ![]() .
.
Непрерывная случайная величина Т, представляющая собой промежуток времени между двумя любыми соседними заявками потока, распределена по показательному закону с параметром l=const (не зависит от времени t).
Функция
распределения![]() , плотность
распределения
, плотность
распределения ![]() , математическое
ожидание (средний интервал времени между двумя соседними заявками)
, математическое
ожидание (средний интервал времени между двумя соседними заявками) ![]()
дисперсия
![]() , среднее
квадратическое отклонение
, среднее
квадратическое отклонение ![]() .
.
6. Непрерывная случайная величина Тоб (время обслуживания одним каналом одной заявки) распределена по показательному закону с параметром m = const.
Функция
распределения ![]() (t ³ 0), плотность
распределения
(t ³ 0), плотность
распределения ![]() (t ³ 0), математическое
ожидание (среднее время обслуживания одной заявки одним каналом, т.е. среднее
время занятости канала)
(t ³ 0), математическое
ожидание (среднее время обслуживания одной заявки одним каналом, т.е. среднее
время занятости канала)
![]()
дисперсия![]() , среднее
квадратическое отклонение
, среднее
квадратическое отклонение ![]() .
.
7.
Показатель нагрузки СМО 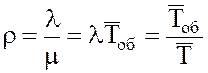 эрланг (0<r<∞).
эрланг (0<r<∞).
8. Вероятность того, что все m каналов свободны:
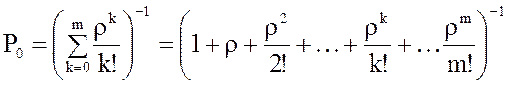 или
или 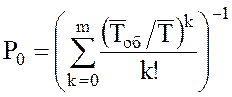 .
.
9. Вероятность
состояний СМО Pk, k=1,2,…,m [8]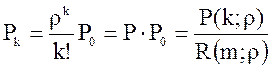 , где
, где
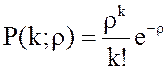 и
и 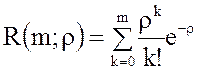 -
табличные значения функции распределения Пуассона, или
-
табличные значения функции распределения Пуассона, или 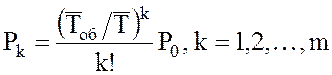 .
.
10. Вероятность того, что все m каналов системы будут заняты, т.е. пришедшая заявка получит отказ (не будет обслужена), значит:
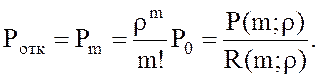
11.
Вероятность того, что пришедшая заявка будет обслужена (вероятность того, что
канал «любой» занят):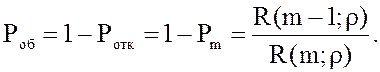
12.
Относительная пропускная способность равна вероятности обслуживания заявки 
13. Абсолютная пропускная способность или среднее число заявок, которое может обслужить СМО за единицу времени:
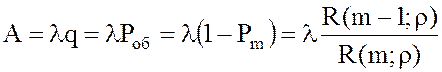
14.
Интенсивность выходящего потока обслуженных заявок (не стоит путать с потоком
обслуживания) 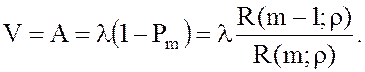
15. Среднее число занятых каналов
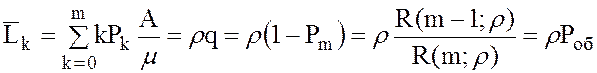 .
.
16. Среднее число заявок под обслуживанием
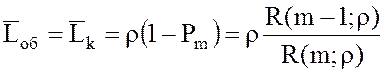 .
.
17. Среднее число заявок, находящихся в СМО:
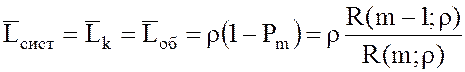 .
.
18. Среднее время пребывания заявки в СМО
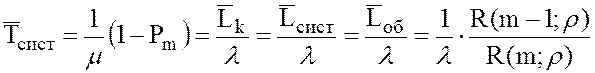 .
.
19. Среднее
время обслуживания заявки, относящееся ко всем заявкам, как обслуженным, так и получившим отказ: 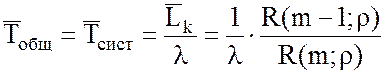 .
.
20.
Среднее время полной загрузки системы 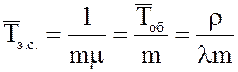
21.
Среднее время простоя канала 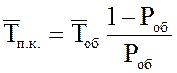 .
.
Пример 3. - Средний интервал между поступающими в
прокатный пункт заявками и запросами на наличие определенных предметов составляет
![]() мин.
мин.
- Принимают заявки два работника, каждый с интенсивностью μ=12 заявок в час.
- С какой интенсивностью должен работать один работник, выполняя работу двух, чтобы доля потерянных требований осталась на прежнем уровне?
- На сколько требуется повысить интенсивность обслуживания двум работникам, чтобы доля потерянных заявок была менее 10%?
Решение. 1. Интенсивность поступления заявок на обслуживание
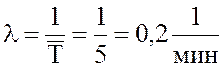 .
.
2. Интенсивность обслуживания каждого работника
μ
= 12 заявок в час = 12/60 = 0,2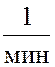 .
.
3.
Показатель нагрузки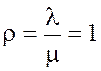 эрланг.
эрланг.
4. Доля потерянных требований для двух работников
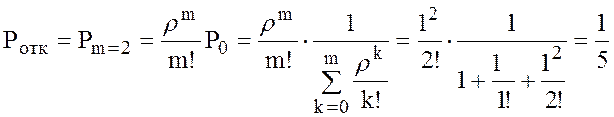 .
.
5.
Доля одного работника с λ = 0,2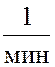 ,
,
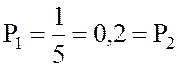 ,
,
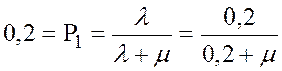 , отсюда μ = 0,8
, отсюда μ = 0,8 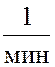 .
.
Следовательно,
один работник, выполняя работу двух, должен трудиться с интенсивностью μ = 0,8 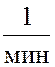 = 0,8∙ 60 = 48 заявки/час, чтобы доля потерянных
требований осталась на прежнем уровне.
= 0,8∙ 60 = 48 заявки/час, чтобы доля потерянных
требований осталась на прежнем уровне.
6. Найдем интенсивность μ, чтобы доля потерянных заказов была меньше 10%.:
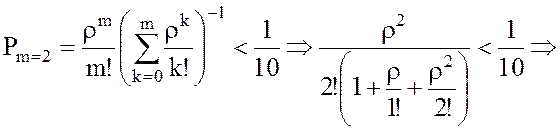
![]()
Принимаем 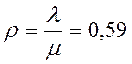 , тогда
, тогда 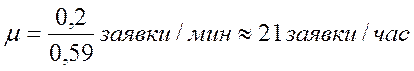 .
.
Следовательно, каждому из двух работников требуется повысить интенсивность на 9 заказов/час (12 + 9) = 21, чтобы доля потерянных заказов была менее 10%.
Пример 4. - Гарантийная мастерская по ремонту холодильников принимает заказы на ремонт по одному телефону.
- Среднее число поступающих в течение часа заказов - 20.
- Среднее время оформления заказа – 4 мин.
- Определить показатели СМО.
- Как они изменятся, если подключить второй телефон?
Решение. 1. Интенсивность поступления потока заказов
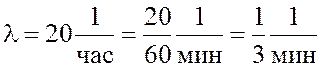 , тогда
среднее время между двумя очередными заказами равно
, тогда
среднее время между двумя очередными заказами равно
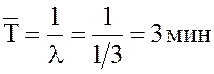 .
.
2.
Среднее время обслуживания ![]() мин, тогда интенсивность
обслуживания
мин, тогда интенсивность
обслуживания 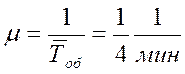 .
.
3.
Показатель нагрузки канала 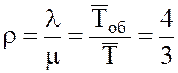 , число каналов m = 1.
, число каналов m = 1.
4. Вероятность того, что все каналы свободны: 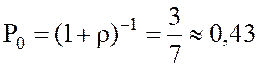 .
.
5.
Вероятность состояния СМО 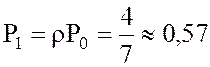 .
.
6. Вероятность отказа Ротк = Р1 ≈ 0,57.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.