(Выделяется диапазон
D4: D9, и с помощью кнопки ![]() находится сумма его элементов,
автоматически записываемого в D10).
находится сумма его элементов,
автоматически записываемого в D10).
22. Вводим в ячейку F6 формулу: = 1/D10 и находим Р0.
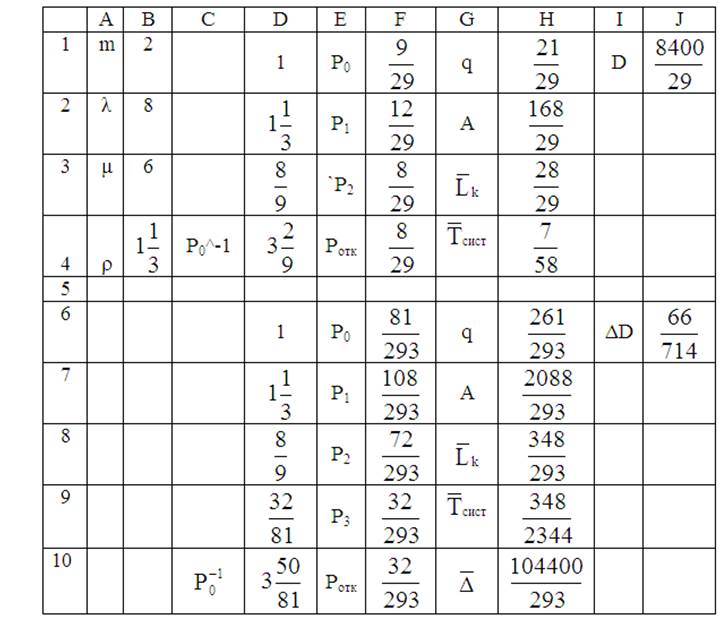
23. Вводим в ячейку Н6 формулу: = 1-F10 и находим q.
24. Вводим в ячейку Н7 формулу: = В2*Н6 и находим A.
25. Вводим в ячейку
Н8 формулу: = В4*Н6 и находим ![]() .
.
26. Вводим в ячейку
Н9 формулу: = H8/B2 и находим ![]() .
.
27. Вводим в ячейку
Н10 формулу: = 50*Н7 и находим ![]() .
.
28. Вводим в ячейку J6 формулу: = Н10- J1 и находим ΔD.
29. ΔD=![]() -D=66,714 < 100. Это означает, что прием на работу третьего мастера
экономически невыгодно.
-D=66,714 < 100. Это означает, что прием на работу третьего мастера
экономически невыгодно.
Показатели эффективности:
Р0
=(1+ρ + ![]() +…+
+…+![]() )-1,
Рk =
)-1,
Рk = ![]() Р0; k=0,1,…m, Ротк
= Pm =
Р0; k=0,1,…m, Ротк
= Pm = ![]() Р0,
Р0,
q = 1- Ротк, A = λ·q, ![]() =
ρ·q,
=
ρ·q, ![]() =
=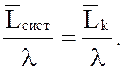
Пример. Подсчитать
показатели эффективности одноканальной СМО с тремя местами (m=3)
в очереди, при условиях: λ=4 заявки/ч, 
Выяснить, как эти показатели изменятся, если увеличить число мест в очереди до m=4.
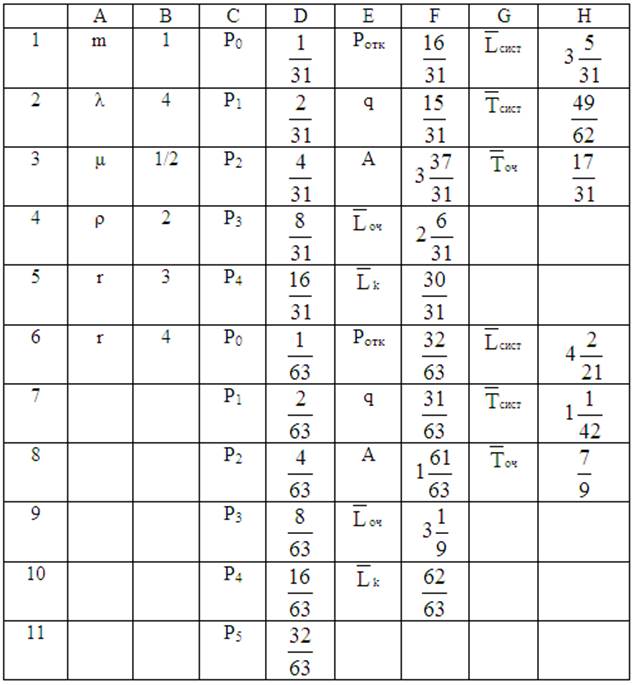
Решение. 1. Вводим в диапазоне А1:А6 условия задачи:
2. Вводим в ячейку D1 формулу: = (1-В2)/1-В2^5 и находим Р0.
3. Вводим в ячейку D2 формулу: = В4^1*D1 и находим Р1, копируем ее в диапазон D3:D5 и находим Р2, Р3 , Р4.
4. Вводим в ячейку F1 формулу: = D5 и находим Ротк.
5. Выделяем ячейки D1:D4 и щелкаем ЛКМ по кнопке ![]() - в ячейке F2
появляется значение q.
- в ячейке F2
появляется значение q.
6. Копируем F2 в ячейку F3 и умножаем на 4, что дает значение А (или вводим в ячейку F2 формулу: = 4*F2 или формулу: =В2*F2).
7. Вводим в ячейку F4 формулу:
=(В4*(1-В4^3(3+1-3*В4)))/(1-В4^5)*(1-В4), находим ![]() .
.
8. Выделяем ячейки D2:D5 и
щелкаем ЛКМ по кнопке ![]() - в ячей ке F5 появится значение
- в ячей ке F5 появится значение ![]() .
.
9. С помощью кнопки ![]() ,выделив F4:F5,
в ячейке Н1 получаем
,выделив F4:F5,
в ячейке Н1 получаем ![]() .
.
10. Вводим в ячейку
Н2 формулу: = Н1/В2, находим ![]() .
.
11. Вводим в ячейку
Н3 формулу: = F4/B2, находим![]() .
.
12. Аналогичным образом находятся показатели эффективности СМО при r=4.
12.4.Одноканальная СМО с неограниченной очередью (с ожиданием)
1. На одноканальную СМО поступает простейший поток заявок с интенсивностью λ = const.
2. Поток обслуживаний также простейший с интенсивностью μ=const>0. Это означает, что непрерывно занятый канал обслуживает в среднем μ заявок в единицу времени.
3. Заявка, поступавшая в момент, когда канал занят, становится в очередь и ожидает обслуживания.
4. Любая пришедшая заявка будет обслужена. Требуется:
5. Построить граф состояний СМО.
6. Найти показатели эффективности СМО.
7. Определить вероятность того, что обслуживания ожидает не более ν заявок.
Решение.1. Состояния СМО нумеруются по числу заявок, находящихся в очереди или обслуживаемых:
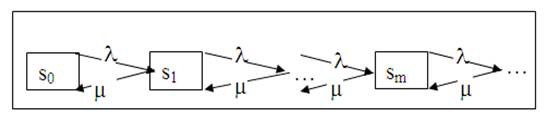
Рис. 12
s0 – СМО свободна (канал свободен);
s1 – канал занят (обслуживает заявку), очереди нет;
s2 – канал занят, одна заявка стоит в очереди;
……………………………………………………………………………
sm –канал занят, m-1 заявка стоит в очереди;
……………………………………………………………………………
2. Показатель нагрузки СМО.
Доказано, что если а)
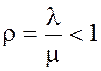 , т.е. среднее число приходящих заявок
меньше среднего числа обслуживаемых заявок (в единицу времени), то вероятности
состояний СМО существуют.
, т.е. среднее число приходящих заявок
меньше среднего числа обслуживаемых заявок (в единицу времени), то вероятности
состояний СМО существуют.
b)
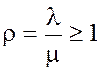 , то очередь растет до бесконечности.
, то очередь растет до бесконечности.
3. Вероятность того, что СМО свободна: Р0 = 1 – ρ, ρ < 1 (Р0 = 0, ρ≥1).
4. Вероятность
состояния любого состояния sk СМО, k = 1,2,… ![]() .
.
5. Вероятность того, что канал занят (степень загрузки канала): Рз.к. = 1 –Р0 = ρ.
6. Вероятность отказа заявке Ротк = 0 (ни одна из поступивших в СМО заявок не получит отказ).
7. Вероятность того, что пришедшая заявка будет принята в систему
( вероятность обслуживания заявки): Рсист = 1 –Ротк = 1.
8. Относительная пропускная способность q = Pсист = 1 – Ротк = 1.
9. Абсолютная пропускная способность A = λ∙q = λ∙1 = λ.
10.
Среднее число занятых каналов – среднее число заявок, находящихся под
обслуживанием, или вероятность того, что канал занят: 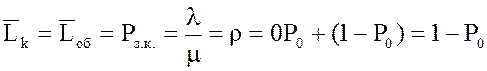 .
.
11.
Среднее число заявок, находящихся в очереди: 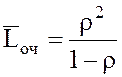 .
.
12.
Среднее число заявок, находящихся в СМО (как в очереди, так и под
обслуживанием): 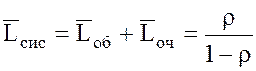 .
.
13.
Среднее время ожидания заявки в очереди 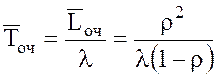 .
.
14. Среднее
время пребывания заявки в системе 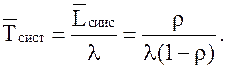
15. Среднее
время обслуживания одной заявки 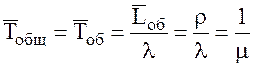
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.