Основные понятия теории массового обслуживания на примерах, страница 2

Пример 1. - Для анализа изменения с течением времени размера текущего фонда компании, ведущей дело по страхованию автомобилей, важно обладать информацией о поступлениях в компанию требований по выплатам в соответствии со страховыми полисами.

- Наблюдение за работой компании в предшествующий период показало, что число поступающих в компанию требований по выплатам за любой промежуток времени длиной r не зависит от момента времени, с которого начинается отсчет промежутка r, а зависит только от его продолжительности. Требования в компанию в любые два непересекающихся интервала времени поступают независимо. В достаточно малые промежутки времени в компанию поступает по одному требованию.

- Ожидаемое число требований, поступающих в компанию за неделю, равно 2.

- Какова вероятность того, что

a) за месяц в компанию поступит 7 требований?

b) за месяц в компанию поступит менее 7 требований?

c) за месяц в компанию поступит не менее 7 требований?

d) за месяц в компанию не поступит ни одного требования?

e) за две недели в компанию поступит хотя бы одно требование?

f) интервал времени между двумя соседними требованиями будет меньше двух дней?

g) интервал времени между двумя соседними требованиями будет не менее двух дней?

Решение. 1. В задаче поток событий – это поток требований по выплатам, поступающим в компанию.

2. Поток будет стационарным, так как число поступающих в компанию требований по выплатам за любой промежуток времени r не зависит от начала этого промежутка, а зависит лишь от его длины.

3. Поток без последствия, потому что требования за любые два непересекающихся интервала времени поступают в компанию независимо.

4. Поток ординарен, потому что в достаточно малые промежутки времени в компанию поступает по одному требованию.

5. Поток является пуассоновским, так как он ординарный без последствия.

6. Поток является простейшим, потому что он стационарный пуассоновский.

7. Принимаем за единицу времени одну неделю.

8. Интенсивность потока l = 2 требований в неделю.

9. Пусть Х(r) – число требований по выплатам, поступающим в компанию за промежуток времени r (недель).

Таким образом, дискретная случайная величина Х(r) может принимать значение m=0,1,2,… .

10. Вероятность поступления в компанию 7 требований по выплатам за месяц вычисляем по закону распределения Пуассона

.

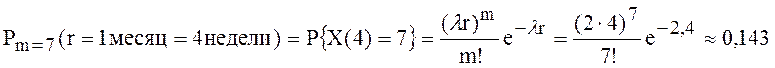11. Вероятность поступления в компанию менее 7 требований по выплатам за месяц:.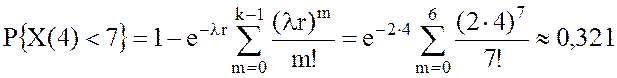

12. Вероятность поступления в компанию не менее 7 по выплатам требований за месяц

13. Вероятность того, что за неделю в компанию не поступит ни одного требования по выплатам .

14. Вероятность поступления в компанию за две недели хотя бы одного требования по выплатам

.

15. Пусть Т – промежуток времени между любыми двумя соседними требованиями по выплатам.

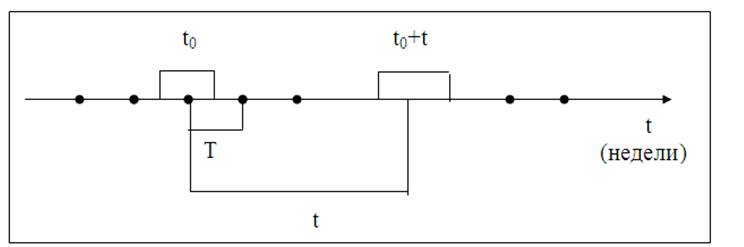
Рис. 6. Временные интервалы t и T

-Таким образом, непрерывная случайная величина Т находится в интервале 0 < T < ∞.

16. Вероятность того, что Т меньше двух дней:

.

17. Вероятность того, что Т не меньше двух дней:

.

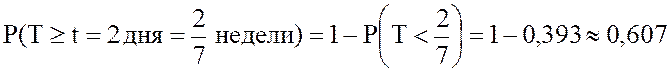10. Показатели эффективности СМО.

10.1. Показатель (коэффициент) нагрузки СМО, интенсивность нагрузки канала, трафик, предельная интенсивность потока заявок, приведенная интенсивность входящего потока r - это среднее число заявок, проходящее за среднее время обслуживания одной заявки одним каналом.

10.2. Показатель (коэффициент) нагрузки СМО, приходящейся на один канал g.

10.3. Приведенная интенсивность потока «уходов» b - это среднее

число уходов из очереди необслуживаемых заявок за среднее время

 обслуживания одной заявки.

10.4. Вероятности состояний СМО Р_k, k=0,1,2,…,m.

P₀ – вероятность того, что все m каналов свободны;

Р₁ - вероятность того, что 1 канал занят;

Р₂ - вероятность того, что 2 канала заняты;

………………………………………………;

Р_k - вероятность того, что все k каналов заняты;

………………………………………………;

Р_m - вероятность того, что все m каналов заняты.