Математика \ Математическое программирование

Задача линейного программирования. Составление экономико-математической модели производства

Страницы работы

4 страницы (Word-файл)

Посмотреть все страницы

Скачать файл

Содержание работы

Задания к аттестации 1

Тема Задача линейного программирования

Номер варианта соответствует последней цифре зачетки

Задание 1

Пусть А=(а_ij) – матрица затрат (а_ij- норма затрат i-го вида сырья на единицу j-го вида продукции);

В=(b_jk) – матрица выпуска (b_jk– количество выпускаемой по плану j-той продукции на k-том предприятии);

С=(с_i) – матрица цен (с_i– стоимость единицы i-го вида сырья).

Используя произведение матриц, определить расход каждого вида сырья и найти затраты на сырье по каждому предприятию

Вариант 1

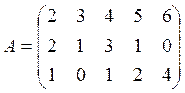
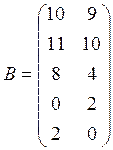
Вариант 2

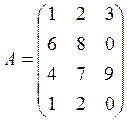
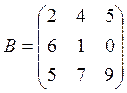
Вариант 3

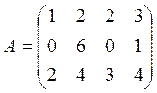
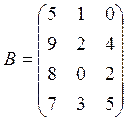
Вариант 4

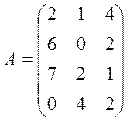
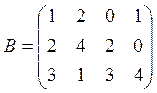
Вариант 5

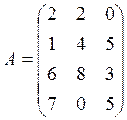
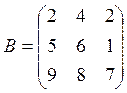
Вариант 6

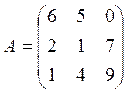
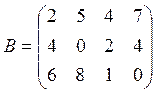
Вариант 7

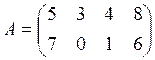
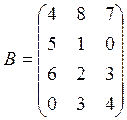
Вариант 8

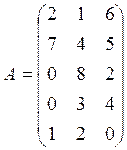
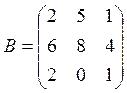
Вариант 9

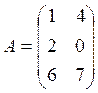
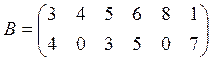
Вариант 10

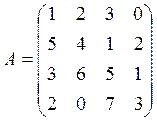
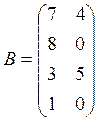
Задание 2

Предприятие производит изделия трех типов А1, А2, А3; при этом используется сырье трех видов S1, S2, S3. Нормы расхода каждого из них на единицу продукции каждого изделия и объем расхода сырья на день заданы в таблице. Найти ежедневный объем выпуска каждого вида изделий, при условии, что сырье используется полностью.

Указание: составьте экономико-математическую модель, обозначив через x_jежедневный объем выпуска каждого вида изделий, запишите условия расхода по каждому типу сырья в виде системы 3-х уравнений с тремя неизвестными:

а₁₁х₁+ а₁₂х₂ + а₁₃х₃ = b₁;

а₂₁х₁+ а₂₂х₂ + а₂₃х₃ = b₂;

а₃₁х₁+ а₃₂х₂ + а₃₃х₃ = b₃;

Полученную систему решить Методом Жордана – Гаусса путем элементарных преобразований расширенной матрицы системы

№ вар.	Тип сырья	Нормы расхода сырья на ед. изделия, у.е.			Расход сырья на день, у.е.
№ вар.	А1	А2	А3	А4	Вi
1	S1	1	3	4	190
	S2	2	1	2	110
	S3	3	2	1	140
2	S1	1	2	3	170
	S2	3	5	2	250
	S3	4	3	4	300
3	S1	1	4	3	260
	S2	4	2	1	180
	S3	5	1	4	290
4	S1	1	5	3	310
	S2	4	2	4	280
	S3	2	3	5	310
5	S1	1	3	5	290
	S2	2	4	1	280
	S3	4	3	3	300
6	S1	1	2	4	190
	S2	3	5	1	310
	S3	4	2	3	260
7	S1	1	3	4	260
	S2	5	4	2	340
	S3	2	3	1	200
8	S1	1	3	2	190
	S2	2	4	5	350
	S3	5	1	3	320
9	S1	1	2	4	270
	S2	3	5	1	330
	S3	5	2	2	310
10	S1	1	2	4	180
	S2	3	3	4	290
	S3	2	4	3	260

Задание №3 по теме Целочисленная задача линейного программирования

Сколько оборудования I и II типов с общей максимальной стоимостью можно разместить на складе S кв.м., если оборудование I типа занимает площадь S1 кв.м., и имеет стоимость C1 у.е., оборудование II типа – S2 кв.м. имеет стоимость С2 у.е. (Оборудования II типа должно быть не менее N2 ед.)?

Ответ задачи линейного программирования привести к целочисленному виду любым возможным методом (методом Гомори, методом Ветвей и границ и др)