The temperature of a substrate, while the covering is drawing on it’s surface, страница 34

Keeping first two members in (8.48) and taking into account (8.49) (E_k = 0), we shall integrate in (8.41)

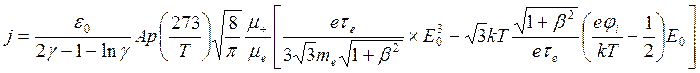          (3.51)

Taking into account (8.50), it is possible to write down

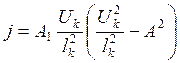                                       (8.52)

where А₁ и A₂ - the factors dependent fromр, Т, In, γ and sorts of working gas.

From the equations (8.29), (8.36) and (8.37) the condition of self-maintenance of the discharge is

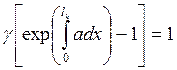                                                 (8.53)

Being limited in (8.48) two members of decomposition and taking into account (8.49), (8.50), we shall receive, that the equation (8.52) gives connection between length of the cathode area and the cathode potential drop Uk. It follows that (8.51). Taking into account (8.50) and (8.52) results in dependence of density of a current on the cathode from Uk and an induction of the magnetic field. The given model approaches for the discharge in which practically the whole voltage drop U occurs in the cathode area [12, 13], that is U≈Uk. On basis of (8.50) and (8.52) the approximation of CVC of the discharge can be constructed and dependence of speed of dispersion on parameters of the discharge can be determined. The equation (8.52) is transcendental and for its decision it is necessary to involve numerical methods. In figure dependences of a current of discharge on the voltage in magnetron sputtering system are resulted at various pressure of working gas and their approximation by the given technique.

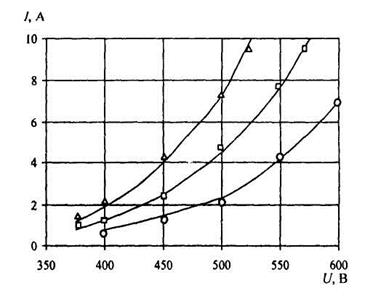
Figure of 8.7 Dependences of a current of discharge on the voltage at various pressure of working gas: ○ - p=0.1 Pa; □ - р=0.25 Pa; Δ - 0.3 Pa (experiment [12]).

Thus, the model of the cathode area of the electric discharge of magnetron sputtering system is offered. Dependence of density of a current on the cathode from the cathode potential drop, an induction of the magnetic field of a sort of working gas for various pressure and temperature of a target is received, taking into account dependence of factor of ionization on energy of electrons and intensity of the electric field.

It is possible to attribute the account of secondary electron emission, processes of ionization and a field of a volumetric charge of positive ions to the advantages of the given method,. Disadvantages of the method are: the model is applicable only for discharge of magnetron sputtering systems in which the whole potential drop occurs practically in the cathode area. Besides, the heterogeneity of density of a current of particles on a cathode - target does not take into account in the given model.

9. Determination of the distribution function of atoms sprayed on a substrate surface

In order to determine later on the heat flow, coming on a surface of a substrate, it is necessary to know, how the sprayed atoms of a cathode - target are distributed on a surface of a substrate. In the given section we shall determine distribution function of the sprayed atoms on a substrate surface in the general case.

We shall conduct calculations for system submitted on fig. 9.1 (a cathode - target is submitted as a disk with radius Rc, a substrate has an arbitrary form, L - distance between the cathode and the substrate).

Fig. 9.1.

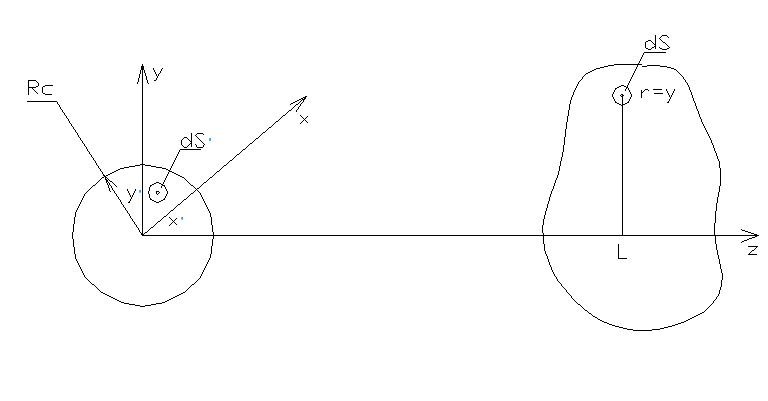The quantity of the atoms getting from an elementary platform of a cathode - target dS' on an elementary platform on a substrate dS in time dt can be presented as

dN=Г₀·f(φ)·dS'·dΩ·dt/2π,                                                          (9.1)

dS'=r'dr'dx' – an elementary platform on a cathode - target;

dΩ – an elementary solid angle, which dS is looked through dS;

dS – an elementary platform on a substrate;

Г₀ – number of the atoms sprayed from unit of a surface of a cathode - target in unit of time;

Г – number of the atoms falling on a surface of a substrate in unit of time;