The temperature of a substrate, while the covering is drawing on it’s surface, страница 32

8.2 Model of the cathode area of discharge

Other model of the processes occuring in a discharge gap is offered in works [12, 13].

The model of the cathode area of electric discharge of magnetron type is offered taking into account processes of secondary electron emission, ionization of atoms, field of a volumetric charge of ions. Dependence of factor of ionization on electron energy and intensity of the electric field is taken into account. Dependence of a current density on the cathode from parameters of the discharge (the cathode potential drop, induction of the magnetic field, etc.) is received. Distinctive feature of the given model from the one considered above, is taking into account the dependence of ionization factor from electron energy and intensity of the electric field.

Results of researches testify to essential influence of speed of firms sedimentation in magnetron sputtering systems on formation of structure of generated coverings. Speed of sedimentation is defined by speed of dispersion v_p, geometry of system, including the distance to a substratel and working pressure. At an assumption of uniform distribution of a current on a sprayed surface of the cathode, speed of dispersion can be expressed for planar magnetron sputtering system as

                                                     (8.25)

where q — density of the material sprayed from unit of the area of the cathode; ρ - density of the precipitable film; τ - time of dispersion. At dispersion in argon

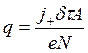                                                      (8.26)

then

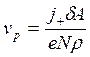                                                      (8.27)

where j₊ – density of an ionic current on the cathode;

δ – factor of dispersion;

А – atomic mass of a sprayed material;

N – Avogadro constant.

The density of an ionic current is connected to thickness of the dark cathode space (DCS) d_DCS and falling of potential U_DCS in DCS by law of Child-Lengmur [12], and also with electron density n_e in plasma and their temperature Т_е by the equation of Bom

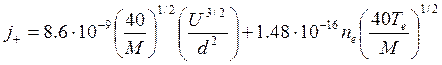               (8.28)

Let's write down system of continuity equations for electronic and ionic components of a current and Poisson equation which is taking into account distortion of an electric field in the interelectrode space as a result of action of a volumetric charge. For the one-dimensional problem in the case, when the flat cathode is placed in the point of origin (х = 0), we have

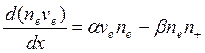                                             (8.29)

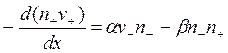                                         (8.30)

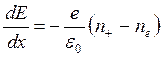                                          (8.31)

                                                        (8.32)

                                                       (8.33)

where n₊, n_е, v₊, v_e, μ₊, μ_е – concentrations, drift speeds and mobility of ions and electrons;

Е – intensity of the electric field;

β – recombination ratio;

ε_о – permittivity;

е – an elementary charge.

Diffusion of the charged particles was not taken into account at recording of this system of equations (8.29) - (8.33), because diffusion of charges in the cathode layer of normal and abnormal glow discharges can be neglected [12, 13]. Ionizing processes are taken into account by using of Tauncend coefficient α, and recombination processes are taken into account by using of the effective recombination ratio β.

A significant role in electron diminution in mixes of electronegative gases can play electron sticking to neutral atoms. To take into account sticking, it is necessary to write down one more equation for balance of negative ions. Thus, the system becomes complicated, and decisions lose clearness, therefore further the results for gases in which sticking does not render appreciable influence on characteristics of the discharge are discussed.

Density of electronic and ionic component of a current are determined as