
Fig. 7.2. Temperature dependence of the accommodation coefficient α, determined by the equation (7.3).
a – Roly and Evans data [71] for Н2 on Fe; b- Hansman data [36]:1 - for SF6 on NiO; 2 - for C2H6 on NiO.
5) Amdur and Guildner [19] have published results of the accommodation coefficient measurements for the systems consisting of inert gases, hydrogen, oxygen and heavy hydrogen on the surfaces of tungsten covered with gas, nickel or platinum at temperatures in a range from 9 up to 100°С. They have presented the results to anothers in the form of linear ratio
αt=α25°[1-δ(t-25°)]. (7.4)
where the temperature factor δ for the systems mentioned above lays in a range between-2,2·10-4 and-9,5·10-4 deg- 1. The formula (7.4) represents experimental results of these authors within ±1 %. However, when constructing diagrams of dependence of the accommodation coefficients from temperature received by other authors the temperature dependence in most cases is nonlinear. However the majority of experimenters did not take into account, that the accommodation coefficient depends not only on absolute values of temperatures, a surface and gas, but also on the size of the chosen temperature difference between the surface and gas (so, in most cases the temperature of gas remains constant and only the temperature of the surface raises). Amdur has chosen in his researches ΔТ≈2 °, that corresponds to the minimal value ΔТ better, than differences to several hundreds of degrees used by other authors.
Various theories of accommodation as will be shown below, are based on rough models and limited to applicability to interaction of atoms of inert gases with a surface of metals. The accommodation coefficients, received from the theory, have more complex temperature dependence, than in the cited empirical formulas.
6) So, Jackson and Mott [393] have offered the formula
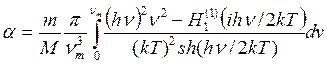 , (7.5)
, (7.5)
Where m and M - weights of atoms of gas and surface, ν - frequencies of fluctuations of a firm body atoms on a surface and νm=k θ/h - the maximal frequency of fluctuations at debye temperature. Hankel’s functions Н1 (1 (ix) at x=h ν/2kT are tabulated in the Janke and Amde’s directory [39].
But Jackson and Mott have made a rough simplification, considering atoms to be firm spheres so the potential of interaction between adsorbed atom and a surface will be V=0 for r> r0 and V = ∞ for r <r0 where r0 - distance of the most rapprochement of atoms.
7) On the other hand, Brown [11] used the formula of Devonshire [17] which has presented potential V on a surface by Morze potential, namely
 , (7.6)
, (7.6)
where Z - amplitude of fluctuations of a lattice, z - coordinate of atom of gas in the direction, normal to the surface and ρ - a constant about 10-8sm. Thus, he has included both attracting force and repulsive force. When taking V on degrees of amplitude Z and limiting only by constant number and a term, which is linear relative to Z, we shall receive
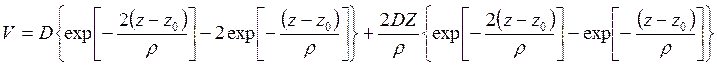 (7.7)
(7.7)
As the amplitude presents only at the first degree, the probability of quantum emission from a lattice is given by the dipole formula. Wave functions of the zero order are the same, as corresponding functions of a two-nuclear molecule in process of dissociation. When assuming Debye distribution of the characteristic oscillation of a crystal, than after complex calculation of probability of transition it is possible to receive the accommodation coefficient as
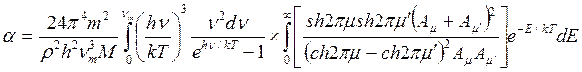 ,(7.8)
,(7.8)
where 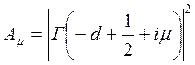 and
and 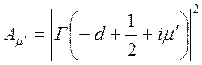
And 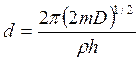 ,
, 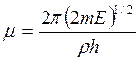 and
and  . (7.9)
. (7.9)
Here parameter D is set by a minimum of potential energy curve V (z) at z=z0 and is approximately equal to heat of adsorption at small degrees of gas covering a surface. When deducting energy of zero fluctuations from D, the heat of adsorption at absolute zero of temperature can be received. Value Е - full energy of the atom of gas, ρ - a constant. The other designations are the same, as in the formula (7.6). Scale function Г (χ) with χ =-d+1/2+i μ can be found also in Janke and Emde’s tables of functions.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.