In magnetron sputtering systems energies of ions of working gas are insignificant, about 300 … 700 eV, therefore on the basis of all aforesaid it is possible to believe, that angular distribution of the sprayed particles in magnetron sputtering systems occurs according to the cosine law.
On fig. 6.4 the settlement of curves describing process of sedimentation at an assumption that the cosine law of emission takes place are resulted, there is no collision of the sprayed atoms with atoms of working gas and the accommodation coefficient is equal to unit.
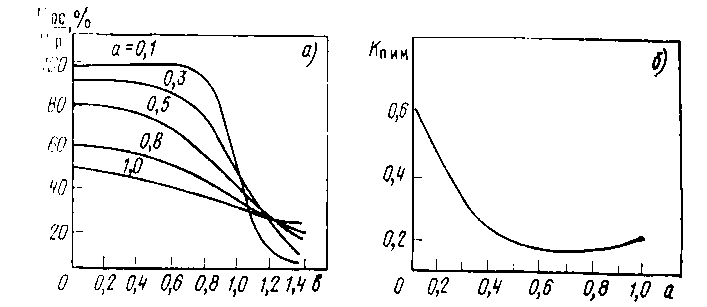
Fig. 6.4 Dependence Vос/Vр on parameter b=r/R (а) and Кп.и.м. on parameter a=D/R (b).
Here Vос and Vр - speeds of sedimentation and dispersion, r distance from the projection of the center of the target to the plane of sedimentation up to a point in which Vос is found, R - radius of a target, a and b - entered dimensionless parameters, Кп.и.м. – the efficiency factor of the target.
7. Dependence of accommodation coefficient on energy exchange between falling atoms and atoms of the surface
The accommodation coefficient is a very important factor, which influence on the quantity of the neutral atoms, which will settle on the substrate, forming a coating and the quantity of reflected particles.
When the atom, energy of which corresponds to the temperature Т0, hits a surface of the firm body, the temperature of which is Т1≠Т0, the energy exchange can take place as result of interaction of atoms of the surface with falling atoms. After staying on the surface according to the average lifetime in an adsorbed condition adsorbed atoms are desorb from the surface with average energy kT2 (fig 7.1).
Fig. 7.1. The scheme of the energy exchange between particles of gas and metal.
Particles of gas with average energy kT0 hit the surface of metal (temperature Т1) and leave it with average energy kT2.
The thermal accommodation coefficient α is a quantitative criterion of this exchange of energy (put in force by Knudsen [43, 44]).
1) If the energy exchange between a falling particle with average energy Е0 and a surface with energy of molecules Е1 is incomplete, particles leave the surface with energy Е2 (Е0≥Е2≤Е1) the accommodation coefficient is determined by
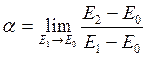. (7.1)
2) In the
general case of a molecule accommodation on a surface the full accommodation
coefficient 
will consist of three
partial accommodation coefficients for the exchange forward
(αforw), rotary
(αrot)
and
oscillatory (αosc)
energies, i.e.
=
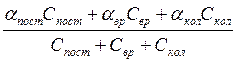, (7.1а)
where Сforw, Сrot, Сosc – contributions in specific molar heat.
3) The temperature contains instead of energy in the most common form of expression for the accommodation coefficient, so
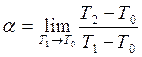. (7.2)
Blodget and Lengmur [56] emphasize, that this definition is strict only on condition that the temperature of the particles leaving the surface Т2, is determined at undistorted maxwellian distribution of particles in the speeds. However this distribution is broken except for a case, when Т0≈Т1.
4) The accommodation coefficient as it was already specified above, depends on the temperature difference ΔТ of gas and surface. Besides, it also depends the area where the temperature size ΔТ lays. The difference ΔТ should be minimal as far as possible.
Aken and Bertram [22] have expressed temperature dependence of the accommodation coefficient α a ratio
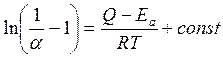, (7.3)
Where energy of activation Еа is received from Frenkel's ratio [25] τ = τ0exp (Ea/RT) which describes temperature dependence of average lifetime in an adsorbed condition τ. Size Q is determined similarly from the equation β = β0exp (Q/RT) for temperature dependence of time of relaxation β (time of relaxation β is that time, which is necessary for the temperature difference between adsorbed gas molecules and a wall drop in е times from initial value). Apparently from fig. 7.2, the ratio (7.3) in most cases present measurements very well, which is illustrated by experimental data of Roly and Evans [73] and Hansman [36]. Apparently, this ratio is equally well applicable both to pure surfaces, and to the surfaces covered with gas.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.