The temperature of a substrate, while the covering is drawing on it’s surface, страница 33

j_e=en_ev_e                                               (8.34)

j₊=en₊v₊                                             (8.35)

The density of a full current will be

j=j_e+j₊                                                (8.36)

We shall limit to consideration the cathode potential drop as function of density of a current then dependencej(Uk) will be, in essence, analogue of current-volt characteristic of discharge. For discharges at low pressure, typical for magnetron sputtering systems (0.1 … 1 Pa), a cathode layer is characterized by surplus of positive ions and a high tension of the electric field, therefore one usually neglects process of recombination and suppose βn₊n_e=0.

The boundary conditions necessary for the decision of system (8.29) - (8.36), are written down as

j₊(0)=γj_e(0)                                                   (8.37)

                                                 (8.38)

where l_k – thickness of a cathode layer;

γ – the generalized factor of outdiffusion under action of ions and photons.

Let the distortion of the electric field in the cathode layer is basically determined by a spatial charge of positive ions n ₊>> n_e [12, 13, 20] then Poisson equation will be written down as

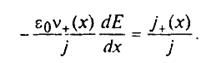                                  (8.39)

Making replacement of variables we shall come to the equation

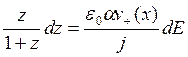                                      (8.40)

with corresponding boundary conditions

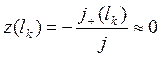
Then after integration the equation (8.40) will be

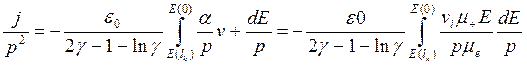           (8.41)

Here р - pressure of gas;

v_i=μ_eα – ionization coefficient.

Asα/p andv ₊ are functionsЕ/р, than it follows from the equation (8.41), that intensity of the electric field is connected to density of a current and pressure by the scaling law E (0)/p=F(j/p2).

In magnetron sputtering system prompting of the magnetic field results in increasing of trajectories of electron movement in an interelectrode interval, hence,  the number of collisions with atoms of working gas, grows. At the presence of the magnetic field transverse electron mobility is:

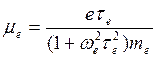                                           (8.42)

where τ_е – average time between collisions of electrons with atoms;

m_е – electron mass;

В – induction of the magnetic field.

It is necessary to know dependence  v_i(E) for integration in (8.41), and the function of electron distribution on energies for the account of this dependence. In the assumption that only elastic collisions of electrons with neutral atoms prevail. In [12] the isotropic part of the function of electron distribution on energies is resulted as

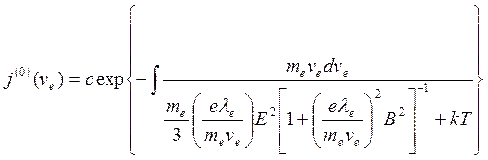                 (8.43)

where m_а – electron mass;

λ_е — average length of electron free path, in the general caseλ_e=λ_e(v_e);

Т – temperature of neutral particles;

К – Boatsman constant;

с — normalizing constant.

If to assume, thatτ_е = λ_е/v_e = const, then

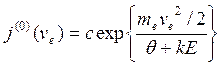,                               (8.44)

where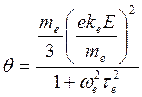  

According to [12, 13] temperature of electrons Т_е= Т+ θ/k. The nonisotropic part of the function of electron distribution on energies will be neglected. Average electron energy is

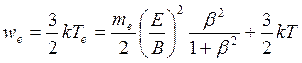,                           (8.45)

here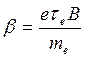

According to [12, 13] frequency of ionizationv, depends on Т_е as follows:

.                           (8.46)

where А — the factor dependent on a sort of gas;

φ_i — potential of ionization of atoms of gas.

Let's designate ξ = кТ/θ. Then

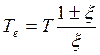                                          (8.47)

As Т_е >> T, then ξ << 1.

Let's substitute (8.47) in (8.46) and, having expanded on degrees ξ, we shall receive:

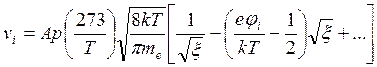                (8.48)

We shall accept linear dependence fromx for distribution of intensity of the electric field [12, 13]:

E(x)=E_o(1-x/l_k)                                   (8.49)

According to (8.38) for the cathode potential drop we shall receive:

U_k=E₀l_k/2                                            (8.50)