The temperature of a substrate, while the covering is drawing on it’s surface, страница 13

On fig. 5.9 and 5.10 curves S (α '), received – by Verner [43] are submitted at dispersion of different targets by ions Hg + and Аг + with low energy (0,5 keV) where α ' is necessary to consider only as a nominal corner of falling as applied by Verner method of dispersion of spherical targets did not allow to make exact definition of hade. Though such factors as an incomplete covering of the surface of a target by the ionic beam and insufficient collimation of the ionic beam, the received results nevertheless are suitable for qualitative discussion of influence of the material of a target on angular laws.

Comparison of the curves received at an irradiation of targets by ions Hg + and Аг + (fig. 5.9 and fig. 5.10), shows first of all, that the angular effect at an irradiation ions Аг + is less, than at an irradiation ions Hg +. Besides in a range of corners 10 ° <α <60 ° the angular effect for the targets concerning to any certain type of a crystal lattice, grows in process of reduction of nuclear weight of the material of a target. For example, for face-centered cubic lattice S (α) _Cu> S (α) _Ag> S (α) _Au, for hexagonal lattice with dense packing S (α) _Ti> S (α) _Zr> S (α) _Hf. It is interesting to note, that this rule does not operate at an irradiation of targets with ions of high energies. For example, at an irradiation of targets from silver and copper ions of Kg + and Ne + with energy 45 keV S (α) _Ag> S (α) _Сu. At an irradiation ions with low energies the least angular effects find out the materials possessing in the greatest factors of dispersion (for example, Сu, Ag, Аu, Ni, Pt) while substances, which are sprayed poorly, find out very strong angular effect (for example, Mo, Fe, Ta). Such complex angular laws for the present have not received a satisfactory explanation in the general theory of dispersion.

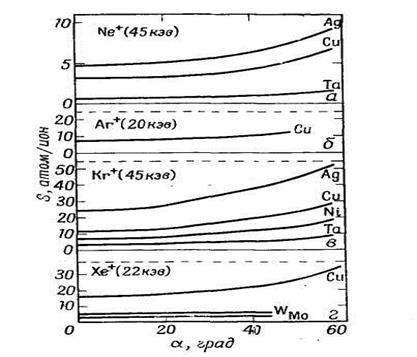
Fig. 5.7 Dependence of the dispersion coefficient S on a hade of ions of inert gases α on various targets.

α – Almen and coll. data [14]; - Roll and coll. data [69]; Almen and coll. data [14]; г – Pitkin’s data [66].

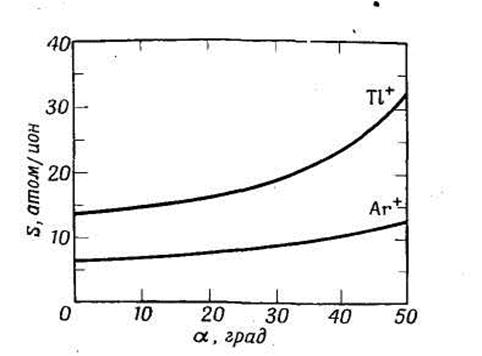
Fig. 5.8 Dependence of the dispersion coefficient S on a hade α for ions Т1 + and Аг + with energy 20 keV, bombarding a copper target (Roll. and coll.[69]).

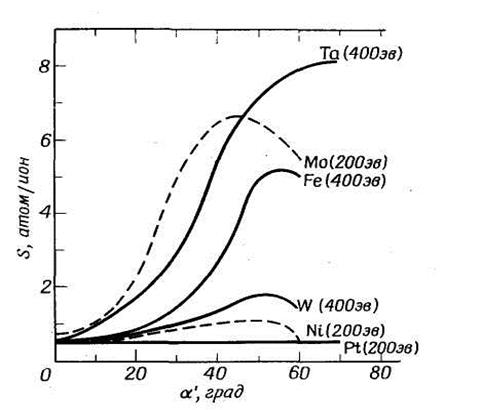
Fig. 5.9 Dependence of the dispersion coefficient S on a conditional hade α ' for ions Hg + on various targets (using of a spherical target has not allowed to define precisely a hade α (Verner [43, 45])).

Fig. 5.10 Dependence of relative dispersion coefficient S α,/S₀ from a conditional hade α ' for ions Аr + on various targets (use of a spherical target has not allowed to define precisely a hade α (Verner [43, 45])).

The review of references [7, 8, 30, 32, 33, 47, 56, 65, 78] also shows, that dependence of the dispersion coefficient on the hade of bombarding ions in different degree influences on the dispersion coefficient for various materials. For example, for iron and molybdenum strong dependence on a hade of ions is observed, for nickel and tungsten - average, for gold, silver and platinum - weak [78] (look fig. 5.11).

Apparently from figure 5.11, with a deviation of a hade of ions from a normal the increase of the dispersion coefficient is observed. And for materials on which the dispersion coefficient renders weak influence, the dependence has almost linear character and on the contrary, there, where the hade renders strong influence on the dispersion coefficient, the area of a strongly pronounced maximum is observed at the corner of falling 40 … 70.

Figure 5.11 Dependence of the dispersion coefficient of various materials on the hade of falling ions of mercury for various energies [78].