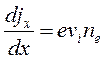The temperature of a substrate, while the covering is drawing on it’s surface, страница 30

                                             (8.14)

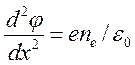
                                         (8.15)

,

where j_х and j_y – density of an electron current, А/m²; b - transverse electron mobility; n_e and n_o - concentration of electrons and neutral particles, m^-3; φ - electric potential, In; v - frequency of ionizing collisions of electrons with neutral particles, s^-1; ε_o - permittivity of vacuum, F/m; σ_i - section of ionizing collisions, m²; σ_o - section of collisions of electrons  with neutral atoms, m²; υ_e – electron speed, km/s.

Considering strong magnetic fields (ω_eτ_e>> 1) and believing, that electrons possess energy, which is essential greater than potential of ionization (it allows to count frequency of ionization constant and not dependent from energy [20, 39]), it is possible to solve system of the equations (8.14) with boundary conditionsφ =0,dφ/dx=E0 at х=0 and to receive expression for current-voltage characteristic (CVC):

I=C(U²-1.5UU₀+0.5U₀²)       (8.16)

where

С=N(p+D);                                                  (8.17)

;                                          (8.18)

D=(S_c/S_n)×G×B,                                             (8.19)

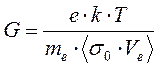;                                         (8.20)

U₀- minimal potential at which the discharge exists (potential of the discharge quenching), dependent on pressure of working gas and value of the induction of the magnetic field (figure 8.8), B, C, N, the D-factors dependent on the induction of the magnetic field; Sк - the area of the sprayed surface of the cathode, m²; a(b) the parameter determining change of classical electron mobility in the magnetic field; Sс and Sn - the areas of section of plasma area and its surface; T - temperature of working gas, K; <σoVe> - speed of ionization of neutral particles by ions of plasma.

Values Sс and Sn are determined as follows:

,                            (8.21)

,                                     (8.22)

,                                          (8.23)

where R_o – radius of a cylindrical surface of the conditional anode, m;

n=l/X_o, where l– half of width of the dispersion zone, m; L – length of the dispersion zone, m

Formulas (8.16) - (8.23) define interrelation between operating (I, U, p, B) and constructive (X₀,S_k, L, l,Sc,Sn) characteristics of magnetron sputtering systems.

It is necessary to note, that the formula (8.16) has been deduced under such initial conditions, whenφ = 0 atх = 0, i.e. without taking into account cathode potential drop. If one takes into account cathode potential drop Uk the formula (8.16) becomes:

I=C[U₂-1.5UU_o+0.5U_o²-0.5U_k(U-U_o)]                            (8.24)

Formulas for CVC contain parameters a(b)and U₀ (B, р) which are not determined analytically. They can be found, approximating experimental CVC with the help of dependence (8.16) or (8.24.). Results of such approximation testify to the good concordance of the theory and experiment [25, 29, 39]. By results of the experimental CVC approximation dependences a(b)=f (B) and dependences of the potential of discharge quenching are found U₀=f (В) and U₀=f (р) (dependence of the potential of initialization or discharge quenching is considered below, see fig. 8.8). In figure 8.6 dependence of parameter a(b)from value of the induction of the magnetic field [38] is shown.

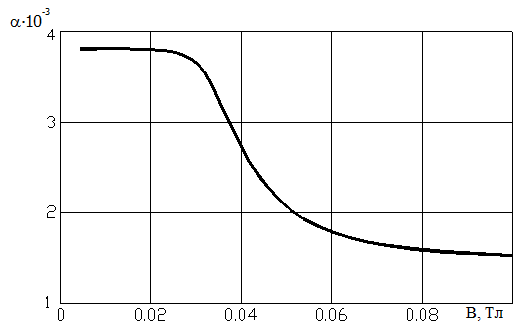
Figure 8.6 Dependence of parameter a(b) from value of the induction of the magnetic field

Apparently, dependence can be divided into three areas:

1)  Area of small sizes of the induction of the magnetic field (<0.03 Tl), parameter a(b)does not practically change with growth of the magnetic induction;

2)        Area of average values the magnetic induction (0.03 … 0.06 Tl), value of the parameter a(b) sharply decreases under the law close to parabolic with growth of value of the magnetic induction;