Аналогично найдем собственные значения оператора квадрата момента импульса
![]() ,
здесь
,
здесь ![]() собственные значения.
собственные значения.
![]()
![]() , где
, где ![]() целое число. Таким образом
целое число. Таким образом ![]() . Собственными функциями являются
полиномы Лежандра
. Собственными функциями являются
полиномы Лежандра ![]() Суммируя все сказанное,
получаем
Суммируя все сказанное,
получаем ![]() для модуля момента количества
движения,
для модуля момента количества
движения,![]()
для проекции на ось имеем![]() причем число
причем число ![]()
Графически все это выглядит следующим образом
![]() Каждому
значению
Каждому
значению ![]() соответствует 2
соответствует 2![]() +1 возможных
+1 возможных
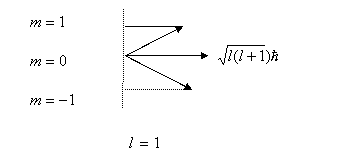 проекций
проекций ![]() ,
т.е. мы имеем дело с
,
т.е. мы имеем дело с
вырождением кратности 2![]() +1.
+1.
Вырождение можно снять, если приложить
внешнее магнитное поле..Действительно,
энергия магнитного момента ![]()
,где ![]() ,
,
в свою очередь ![]() есть магнетон Бора. В результате
уровень расщепляется на
есть магнетон Бора. В результате
уровень расщепляется на ![]() подуровней, между
которыми могут происходить переходы с излучением или поглощением квантов
электромагнитного излучения с энергией
подуровней, между
которыми могут происходить переходы с излучением или поглощением квантов
электромагнитного излучения с энергией ![]()
![]() . Это явление
. Это явление
получило название эффекта Зеемана, а в твердых телах явление парамагнитного резонанса.
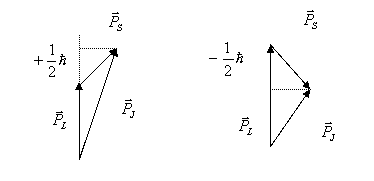 Известно, что кроме орбитального
момента электроны обладают собственным механическим моментом или спином.
Особенность спинового момента заключается в том, что его проекция на выбранное
направление может принимать только два значения
Известно, что кроме орбитального
момента электроны обладают собственным механическим моментом или спином.
Особенность спинового момента заключается в том, что его проекция на выбранное
направление может принимать только два значения ![]() .Величина
самого момента
.Величина
самого момента ![]() , причем
, причем ![]() . Для одного электрона спиновой и
орбитальный моменты складываются векторно, образуя полный момент
. Для одного электрона спиновой и
орбитальный моменты складываются векторно, образуя полный момент ![]() . Так как
. Так как
спиновой момент может иметь лишь две ориентации, то и полный
момент ![]() имеет
два различных значения. В результате энергетический уровень расщепляется
имеет
два различных значения. В результате энергетический уровень расщепляется
на два подуровня, спектральная линия состоит из двух близких по длинам волн линий
(говорят о спектральном дублете). Значит спин задает мультиплетность энергетического
уровня. Она равна 2S+1.
Значение квантового числа ![]()
![]() определяет тип терма S, P. D и
т.д.
определяет тип терма S, P. D и
т.д.
В качестве примера рассмотрим атом гелия, в котором имеется два валентных электрона.
Каждый из электронов имеет орбитальный момент, величина
которого определяется энергетическим уровнем с номером n
(L=0.1…n-1) и спиновым моментом
S. Имеется две возможности для сложения этих моментов в
суммарный момент атома. Для легких атомов складываются отдельно орбитальные
моменты валентных электронов(![]() ), отдельно
спиновые моменты (
), отдельно
спиновые моменты (![]() ),а затем они складываются
в суммарный момент атома
),а затем они складываются
в суммарный момент атома ![]() (L-S связь). Рассмотрим основное
состояние атома гелия. Оба электрона находятся в состоянии с n=1,поэтому
орбитальный момент l=0. Спиновые моменты могут в сумме
давать 0, когда спины направлены в противоположные стороны S=0.
(L-S связь). Рассмотрим основное
состояние атома гелия. Оба электрона находятся в состоянии с n=1,поэтому
орбитальный момент l=0. Спиновые моменты могут в сумме
давать 0, когда спины направлены в противоположные стороны S=0.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.