Квантовая механика, металлы и полупроводники. Волновые свойства частиц (волны де Бройля), страница 3

 Для упрощения выкладок рассмотрим одномерное волновое уравнение

, и

 Найдем вторые производные по времени и по координате от нашей волновой функции:

, (- аналогично по времени

,подставим наши выражения в волновое уравнение и получим:

 Cокращаем уравнение на временной множитель, подставляем E= 

 в итоге получаем

 В свою очередь , где Е_k - кинетическая энергия, Е- полная энергия и U – потенциальная энергия тела. Окончательно имеем

 Последнее выражение и есть одномерное стационарное уравнение Шредингера.

 Обобщение на трехмерный случай не представляет труда

ΔΨ( r )+Ψ(r )=0

 Где Δ -оператор Лапласа Δ=

Частица в потенциальном ящике.

 В качестве примера рассмотрим решение уравнения Шредингера в одномерном случае для частицы массой m , находящейся в потенциальном ящике. Потенциальным ящиком называется область пространства, ограниченная бесконечно высокими стенками.

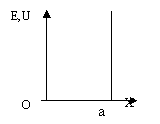Для этого случая имеем:

 U=

0≤ X ≤ a, U= 0

a ≤ X ≤, U=

Вероятность нахождения частицы вне потенциального барьера равна 0,    следовательно

в областях 1 и 111 волновая функция равна 0.

Во второй области уравнение Шредингера принимает вид

, введем обозначение , в результате чего наше уравнение приобретет вид:

 Решение этого уравнения хорошо известно

 Постоянные А и В определяются из граничных условий

 и

Из первого условия имеем: 0= В, из второго – A sin(k a)= 0

Чтобы волновая функция не стала тождественным 0, придется приравнять 0 значения sin(k a)=0. Из этого следует, что k приобретают дискретные значения k a= n, а вместе с этим дискретные значения приобретает и энергетический спектр частицы

E _n=( n= 1, 2, 3,…)

 Отсюда делаем вывод, что при ограниченном движении частицы ее энергетический спектр становится дискретным.

Определим расстояние между соседними энергетическими уровнями: