Квантовая механика, металлы и полупроводники. Волновые свойства частиц (волны де Бройля), страница 20

 Вблизи минимума энергии имеем разложение

 Квадратичная зависимость энергии от волнового вектора  характерна для параболических зон. Для массы электрона вблизи минимума энергии получаем выражение

.

 Для ширины разрешенной энергетической зоны было получено соотношение

, отсюда  и .

 Отсюда следует, что эффективная масса электрона зависит от ширины разрешенной зоны.

 Аналогичным образом рассмотрим энергию электрона вблизи максимума

Опять рассмотрим разложение вблизи этого максимума, для этого введем новое волновое число и тоже для других координат. Тогда

,  и т.д.

 В этом случае для энергии электрона имеем  и эффективная масса

 Вблизи максимума энергии получаем отрицательное значение массы для электрона, во внешнем поле он будет двигаться вдоль по полю, т.е. будет вести себя как положительная частица. Формально вводится понятие квазичастицы, которую назвали ‘дыркой’. Ей приписали положительный заряд, по модулю равный заряду электрона, и положительную эффективную массу.

 Для S состояний электрона вблизи максимума и минимума изоэнергетические поверхности представляют из себя сферы, поэтому эффективная масса оказывается скалярной величиной и не зависит от направления в кристалле. В общем случае эффективная масса носит тензорный характер.

Концентрация носителей тока в собственном полупроводнике.

В собственных полупроводниках концентрация электронов и дырок равны n=p.

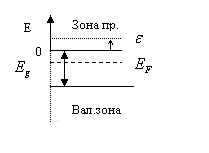Рассчитаем сначала концентрацию электронов 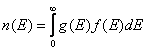, здесь Е энергия электронов в зоне проводимости, f(E) –функция распределения Ферми-Дирака.

Начало отсчета энергии совместим с дном зоны проводимости.

Энергия электрона равна в этом случае , энергия Ферми отрицательна и равна  В этих обозначениях имеем

,

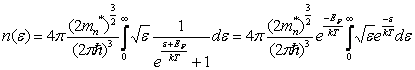здесь мы учли, что в большинстве полупроводников электронный газ является невырожденным. В последнем интеграле произведем замену переменных . В этих переменных 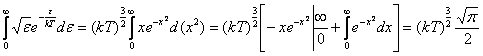.Окончательно получаем

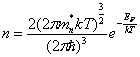.По аналогии найдем концентрацию дырок. 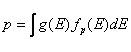, функция распределения

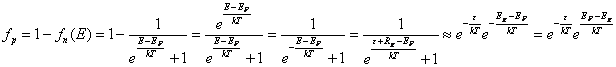, здесь учтено, что энергия дырки в нашей системе отсчета энергии  и энергия Ферми отрицательна. Концентрация дырок 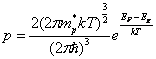. Положение уровня Ферми найдем из равенства концентраций электронов и дырок , или

, что дает положение уровня .

В частном случае равенства эффективных масс электронов и дырок уровень Ферми лежит посередине запрещенной зоны  В этом случае 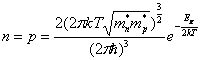 и для проводимости собственного полупроводника получаем следующую зависимость