Рассмотрим результат применения этой формулы для ряда конкретных случаев.
а) классический газ
линейные размеры сосуда, в котором заключен газ а= 0.1м, масса молекул
m=5.3 10-26 кг. Имеем ∆En+1,n=10-40 Дж=6 10-20 эВ. В свою очередь тепловая энергия тех же молекул ε =к Т =1.38 10-23 300 = 4.2 10-21 Дж =2.5 10-2 эВ. Делаем вывод, в этом случае энергетический спектр можно считать непрерывным и волновые свойства молекул не принимать во внимание
б) электрон в куске проводника.
Линейные размеры проводника а= 0.1 м, масса электрона m=9.1 10-31 кг
∆En+1,n= 3 10-17 эВ, что также существенно меньше тепловой энергии.
Однако, в этом случае мы имеем дело с так называемыми фермионами(с частицами с полуцелым спином), поэтому дискретный энергетический спектр сказывается на характере заполнения уровней, а также на среднюю энергию электронов в металле.
в) электроны в атомах.
В этом случае область локализации электрона а= 10-10м, ∆En+1,n= 25 эВ. Значит, дискретность энергии весьма существенна.
Нам осталось определить постоянную А, для чего воспользуемся условием нормировки волновой функции:
,
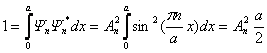А=
.
Окончательно имеем 
.
Рассчитаем вероятность нахождения частицы, находящейся на энергетическом уровне с номером n, внутри потенциальной ямы.
|
w =|Ψn|2
=
Отметим еще одно свойство собственных функций.
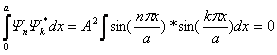
Таким образом, волновые функции, соответствующие
разным собственным состояниям, являются ортогональными
Туннельный эффект.
Рассмотрим прохождение частицы сквозь потенциальный барьер, причем полная энергия этой частицы меньше величины потенциального барьера.
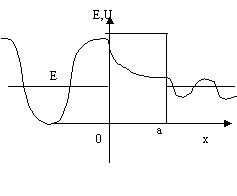В области 1 (
) U=0
В области 2 
, U=U0
В области 3 
. Вновь введем обозначение k2=
,
для областей 1,3 получим известное уравнение
, решение которого имеет вид
Для области 2 Е< U0 , поэтому для нее введем обозначение
.
Уравнение для второй области приобретает вид 
.
Решение этого уравнения записывается следующим образом
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.