Квантовая механика, металлы и полупроводники. Волновые свойства частиц (волны де Бройля), страница 19

3. Ширина зоны разрешенных энергий определяется величиной обменного интеграла А. Для рассмотренного случая примитивной кубической решетки

Е_max=E₀+C+6А   (когда cos(k_xa)=cos(k_ya)=cos(k_za)=1)

E_min=E₀+C-6A   (когда cos(k_xa)=cos(k_ya)=cos(k_za)=-1) и

∆Е=Е_g=12A

4. Величина обменного интеграла будет расти для электронов, находящихся на более высоких энергетических уровнях, т.е. для этих уровней ширина разрешенной области будет шире.

5.Зоны разрешенных энергий в общем случае будут разделены зонами запрещенных энергий.

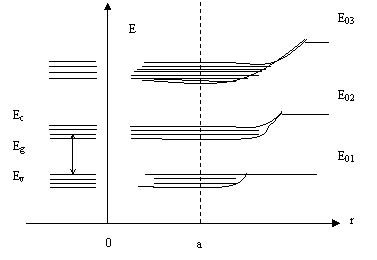 6.С ростом энергии ширина зон разрешенной энергии увеличивается, а ширина зон запрещенных энергий уменьшается.

 Для простой кубической решетки  и А<0

 E=E₀-C-2(cos(k_xa)+cos(k_ya)+cos(k_za)

б) Рассмотрим р состояние электрона в атоме. Для этих состояний полином Лежандра Р₁=соsx.

 В этом случае перекрывающиеся функции имеют

разные знаки, поэтому для р состояний А>0 и для

энергии электрона имеем:

 E=+2|A|

Эффективная масса электрона.

Дырки.

 Для свободного электрона имеем , импульс определим из соотношения де-Бройля . Энергия свободного электрона связана с его волновым числом .

 Эта зависимость получила название закона дисперсии .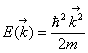

 Возьмем дифферинциал от левой и правой частей

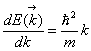, откуда

 С учетом этого значения k импульс электрона перепишется следующим образом

 и для скорости имеем

 Применим полученное выражение для движения электрона под действием внешней силы F. Эта сила вызывает ускорение частицы

 Определим

, или

 Стало быть .

 Суммируя все выкладки, получаем:

Наше уравнение имеет вид 11 закона Ньютона, если определить массу частицы с помощью  выражения

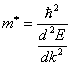
 Для свободной частицы 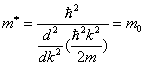 по прежнему равна массе покоя.

 Рассмотрим влияние поля кристаллической решетки на поведение электрона. Рассмотрение опять проведем для s состояния электрона в простой кубической решетке.

E=E₀-C-

 За начало отсчета энергии примем Е₀-С, тогда энергия электрона будет равна:

 Минимальное значение эта энергия принимает при k_x=k_y=k_z=0, ()