Квантовая механика, металлы и полупроводники. Волновые свойства частиц (волны де Бройля), страница 17

мала по сравнению с его кинетической энергией . Следовательно, решение в этом случае будет мало отличаться от решения уравнения для свободного электрона:

 и

С учетом этого замечания представим саму функцию и потенциальную энергию в виде разложения в ряды. Так как эти функции периодические, то естественно разложить их в ряды Фурь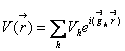е. , где - вектор обратной решетки,  малый параметр.

 Аналогично 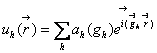. Эти разложения подставляем в уравнение Шредингера.

 

 Учтем, что оператор  действует только на координаты:

 

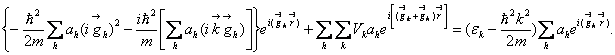
 Перегруппируем члены:

 

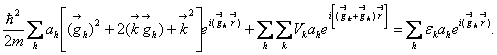
 Наше уравнение превратилось в бесконечную систему уравнений для коэффициентов а_h.

, или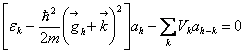

 Решение этой системы уравнений начнем с рассмотрения свободных электронов, в этом случае V_k=0, ψ=aи . Имеем: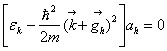, возможны два варианта, либо все а_h=0, включая а₀(случай отсутствия электрона), либо  и а₀=1, а_h=0.

***

Приближение сильной связи.

 В этом приближении электрон проводит большую часть времени около своего иона, поэтому его состояние описывается с помощью волновых функций изолированного атома, которые подчиняются уравнению Шредингера

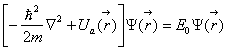
 В кристалле эта функция зависит от координат следующим образом

,

где  координаты конкретного атома, к которому принадлежит электрон. Будем считать, что в кристалле волновая функция будет мало отличаться от Ψ для изолированного атома:

.

 Для того, чтобы волновая функция имела вид функции Блоха коэффициенты разложения а_n должны иметь вид- . В результате получаем

 Потенциальная энергия электрона в кристаллической решетке U в этом случае можно представить в виде суммы , где добавочный член  учитывает наличие других атомов в своих узлах кристаллической решетки. С учетом всего сказанного уравнение Шредингера приобретает вид:

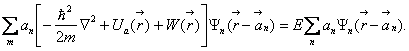 С учетом уравнения Шредингера для изолированного атома наше уравнение упрощается

, или .

Найдем среднее значение энергии электрона <E₀-E>. Для этого умножим наше уравнение на комплексно сопряженную функцию  и проинтегрируем по всему объему кристалла.