Квантовая механика, металлы и полупроводники. Волновые свойства частиц (волны де Бройля), страница 16

б).Одноэлектронное приближение.

 Рассмотрим потенциал, создаваемый ионами в узлах кристаллической решетки. Каждый из электронов находится в поле всех ионов кристаллической решетки, плюс к этому мы должны 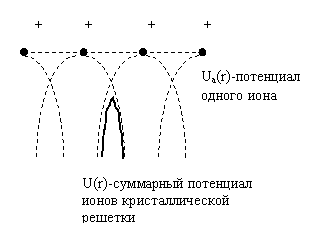учесть взаимодействие электронов друг с другом:

. Суть одноэлектронного приближения заключается в том, что потенциальная энергия взаимодействия электронов учитывается с помощью введения усредненного эффективного поля U_eff(r), которое должно наилучшим способом описывать действие всех остальных электронов на данный. Введение такого поля позволяет рассматривать отдельно движение каждого конкретного электрона.

 Уравнение Шредингера разбивается на сумму уравнений, каждое из которых описывает движение одного электрона:

.

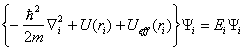 При таком рассмотрении волновая функция ансамбля электронов Ψ(r₁,r₂,…r_n) может быть представлена в виде произведения отдельных волновых функций:

Ψ(r₁,r₂,…r_n)=Ψ(r₁)Ψ(r₂)…Ψ(r_n).

 Из этого следует, что совокупность электронов представляет из себя ансамбль невзаимодействующих частиц (электронный газ).

Теорема Блоха.

Из приведенного рассмотрения следует, что потенциальная энергия электронов есть периодическая с периодом трансляционного вектора прямой решетки функция координат

,

следовательно, волновые функции, соответствующие этим координатам, могут отличаться друг от друга на некоторый постоянный множитель:

, причем .

 Для нахождения явного вида С произведем два последовательных смещения на и на

 Этому условию сложения удовлетворяет экспонента , где -волновой вектор, описывающий движение электрона (k≈1/м).

.

 Выражение называется функцией Блоха, где  в свою очередь есть периодическая функция координат

 Сравнивая функцию Блоха  с волновой функцией для свободных электронов

  видим, что вместо постоянного множителя А (АА^*=1 и вероятность нахождения электрона постоянна во всем пространстве) имеем множитель, зависящий от координат электрона, что приводит к модуляции распределения электронов в кристаллической решетке.

 Подставим функцию Блоха в уравнение Шредингера

, здесь  суммарная потенциальная энергия электрона. Предварительно вычислим

 , аналогично

 , с учетом этого наше уравнение Шредингера примет следующий вид:

 Решение этого уравнения удается найти с помощью различных приближений.

Приближение слабой связи.

 В приближении слабой связи предполагается, что потенциальная энергия электрона