Квантовая механика, металлы и полупроводники. Волновые свойства частиц (волны де Бройля), страница 12

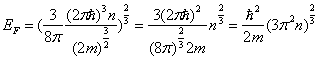
Эта формула справедлива при температуре .

Распределение Ферми-Дирака.

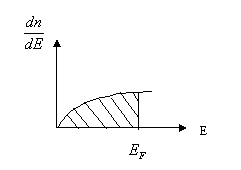Определим число состояний для электронов, приходящихся на малый интервал энергии.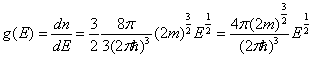

Известно, что все уровни вплоть до энергии Ферми

заняты электронами, т.е. вероятность их заполнения равна 1, все дальнейшие уровни свободны, для них вероятность заполнения равна 0. Электроны в металле подчиняются особой статистике-статистике Ферми-Дирака. Вероятность заполнения уровней в этом случае равна .

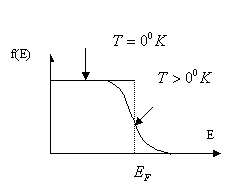
График этой функции выглядит следующим образом

Ширина переходной области порядка kT. Для

металлов можно ввести температуру Ферми

, при концентрации электронов ~ величина этой температуры составляет~, что существенно больше температуры плавления любого металла. Значит электронный газ в металлах подчиняется статистике Ферми-Дирака при любой температуре. Про такой газ говорят, что он вырожденный. Напротив, в полупроводниках концентрация электронов ~.

Это означает, что уже при малых значениях Е, , поэтому мы получаем переход к статистике Максвелла-Больцмана  В этом случае электронный газ является невырожденным.

Зная функцию заполнения, можно вычислить энергию электронов

.

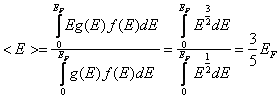Также как и энергия Ферми средняя энергия электронов в металле составляет единицы электронвольт.

Теплоемкость электронного газа.

 Статистика Ферми-Дирака для электронов приводит еще к одному важному следствию-теплоемкость электронного газа оказывается существенно меньше классической величины.

 Рассчитаем энергию электронов при температуре Т, отличной от 0 градусов Кельвина.

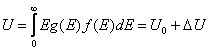 , где 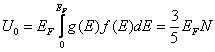 энергия электронов при 0 Кельвина, причем эта энергия не зависит от температуры.

по определению .

Для того чтобы вычислить последний интеграл, используем постоянство частиц в металле 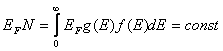, и 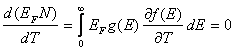.С учетом последнего равенства для теплоемкости получаем следующее равенство

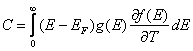
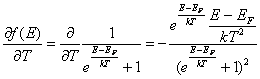Вычислим  и подставим в наш интеграл

.

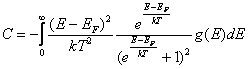Введем новую переменную , Новые пределы интегрирования

при Е=0    , другой предел . Добавочно учтем, что  отлична от 0 только при энергиях близких к энергии Ферми, поэтому .