Квантовая механика, металлы и полупроводники. Волновые свойства частиц (волны де Бройля), страница 5

 . Для нахождения коэффициентов a_1,2,3 и b_1,2,3 воспользуемся свойством непрерывности функции и

ее первой производной, но прежде сделаем одно замечание. После прохождения

барьера частица удаляется в бесконечность, а это значит, что в решении для области 3 имеется только волна, распространяющаяся в положительном направлении оси x. Следовательно  . Аналогично запишем решение для области1 , где первый член-это падающая на барьер волна, а второй -отраженная от барьера волна. В области 2 одно решение экспоненциально уменьшается, а второе таким же образом растет. Нарастающее решение не имеет физического смысла, поэтому b₂ =0 , и решение для этой области имеет вид . Прежде чем находить эти коэффициенты, установим некоторые соотношения между ними.

Коэффициент прозрачности барьера D=, коэффициент отражения

T=.между ними существует дополнительная связь D+T=1

Воспользуемся условием непрерывности волновой функции

a₁+b₁=a₂,

Теперь используем условие непрерывности производной волновой функции

 и . Найдем решение наших уравнений

а₁+ b₁=a₂

a₁- b₁=        

Сложим и вычтем эти уравнения 

В свою очередь , откуда  или . Возведем обе части в квадрат , откуда для коэффициента прозрачности барьера имеем D=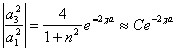, где

Величина

Аналогичным образом можно определить коэффициент отражения

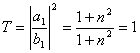
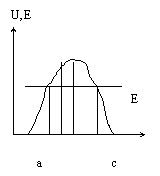
Обобщим наши результаты на барьер произвольной формы.

Барьер произвольной формы можно представить как совокупность бесконечно узких барьеров прямоугольной формы. В этом случае прозрачность барьера

Туннельный эффект объясняет явление автоэлектронной эмиссии, работу туннельного диода и т.д..

Собственные значения и собственные функции

уравнения Шредингера.

Перегруппируем уравнение Шредингера

следующим образом

и введем оператор полной энергии тела (Гамильтониан)

В этих обозначениях стационарное уравнение Шредингера приобретает вид