Квантовая механика, металлы и полупроводники. Волновые свойства частиц (волны де Бройля), страница 7

, , или

Видим, что результат действия этих операторов на волновую функцию зависит от порядка сомножителей. Такие операторы называются некоммутативными.

 Другой пример ,

В этом случае  имеем , т.е. в этом случае результат не зависит от порядка операторов. Вспоминая соотношение неопределенностей Гейзенберга, приходим к выводу, если произведение операторов не коммутативно, то физические величины им соответствующие не могут быть измерены абсолютно точно одновременно.

Оператор момента количества движения.

Из механики известно, момент импульса частицы определяется векторным произведением  L=. или в проекциях на оси координат

,    .

Рассмотрим произведение

И аналогично

Найдем разность этих произведений, учитывая перестановочные соотношения между операторами

Совершая циклическую перестановку переменных X,Y.Z, получим еще два аналогичных выражения

и .

Из этих соотношений следует, что можно однозначно определить лишь одну составляющую момента импульса. Однако, имеется еще одно соотношение для момента импульса

 

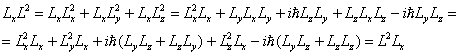
Следовательно, можно одновременно измерить одну компоненту момента импульса и квадрат момента импульса.

Собственные значения и собственные функции оператора момента импульса.

Нахождение собственных функций удобнее проводить в сферической системе  координат 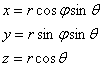                           Преобразуем, для примера , компоненту            ,  , в этих координатах квадрат момента импульса         будет иметь вид , где есть оператор Лапласа для сферы , и он

равен ,             

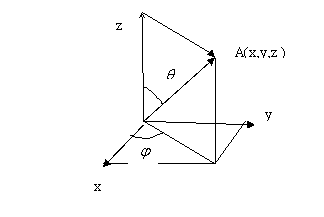
Для нахождения собственных значений и

собственных функций данных операторов

представим волновую функцию в виде произведения

В результате имеем

, или

, откуда получаем

, решением последнего уравнения является

, добавочным условием является требование периодичности . Это приводит к тому, что .

Следовательно, собственные значения оператора , где m целое число (0,).