Квантовая механика, металлы и полупроводники. Волновые свойства частиц (волны де Бройля), страница 2

ΔE Δt. Эти соотношения и есть соотношения неопределенностей Гейзенберга. Из них видно, что принципиально нельзя одновременно измерить абсолютно точно координату частицы и ее скорость, что приводит в волновой механике к ряду существенных последствий: 1)теряется понятие траектории частицы; 2) частицы становятся неразличимыми (тождественными), что, в свою очередь, приводит к тому, что эти частицы подчиняются новым статистикам, отличным от статистики Максвелла.

Характерные размеры атомов.

Зададим среднее расстояние электрона от протона порядка «а», тогда неопределенность импульса электрона будет равна Δ р ≈/a . Принимая импульс электрона  по порядку равным его неопределенности, получим кинетическую энергию равной Е _к= p²/2m=h²/2ma² .В системе СГС полная энергия электрона равна Е _пол= h²/2ma²-е²/a , где е заряд электрона. Система будет находиться в устойчивом состоянии, если ее полная энергия минимальна.

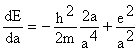=0

Отсюда для размеров атома получаем

а это есть радиус первой боровской орбиты. Зная среднее расстояние электрона от атома, можно вычислить его энергию:

Отрицательная полная энергия говорит о том, что электрон находится в связанном состоянии и для его удаления от ядра необходима эта энергия, поэтому она называется энергией ионизации атома.

Физический смысл волн де-Бройля.

Рассмотрим опыт Тартаковского-Томсона. Через фольгу будем пропускать по одному электрону. Совершенно неясно в какое место экрана попадет этот электрон. Следующий электрон, в общем случае, может попасть в другую точку.

Картина начнет приобретать упорядоченный характер дифракционных колец только при достаточно большом количестве электронов. Это указывает на статистический характер распределения координат рассеянных электронов. Откуда следует, что волновая функция описывает движение электронов вероятностным образом.

Вероятность попадания электрона в заданную точку с помощью волновой функции определяется квадратом волновой функции:

 dP = Ψ•Ψ^*•d V , здесь Ψ–волновая функция, Ψ^*-комплексно-сопряженная функция

dV –элемент объема вблизи этой точки

 В случае  дискретных значений  параметров, характеризующих состояние объекта, вероятность нормируется на вероятность достоверного события, которая равна 1

Р=∫∫∫Ψ Ψ^* dV =1  или  ∫∫∫ [Ψ ]²dV =1

 Интегрирование ведется по всему пространству возможных значений параметров.

Уравнение Шредингера.

 Рассмотрим волновую функцию свободной частицы

Ψ = А exp [-i (]

 Как всякая волновая функция она является решением волнового уравнения

ΔΨ= 1/v²

 Представим волновую функцию в виде произведения временной и координатной компонент

Ψ=А exp [-i (]=exp [-i ()] А exp(-)=exp-i ()] Ψ(r )