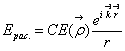Квантовая механика, металлы и полупроводники. Волновые свойства частиц (волны де Бройля), страница 10

,

здесь  координата рассеивающего атома. Учет фазовых соотношений рассеянных волн позволяет определить направления, по которым рассеянные лучи будут усиливать друг друга. Введем вектора - расстояние от начала координат 0 до точки Р, -положение атома в кристаллической решетке, - расстояние от этого конкретного атома до точки наблюдения Р. Пусть », тогда =-;

 r ≈ R-ρ_mnpcosθ где cosθ=cos(). Угол θ в наших предположениях мал, поэтому рассеянное излучение распространяется вдоль направления . Определим фазу рассеянной волны:

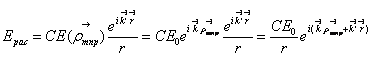    , E₀ пропорционально интенсивности падающей на кристалл волны. Для фазы отраженной волны получаем выражение

φ=.

 С учетом этого для рассеянной волны получаем:

 , в этом выражении учтено, что R≈r, модули  и .

 Мы получили рассеянное излучение от одного атома. Осталось просуммировать по всем N рассеивающим центрам, где N полное число атомов в кристалле. Для этого надо сложить фазовые множители

А=, здесь А амплитуда рассеяния, ее максимальное значение А=N.

 Вектор . Амплитуда рассеяния максимальна, если , где n-целое число (имеем интерференционный максимум). Если  не будет соответствовать .этому условию, то при большом числе атомов N амплитуда рассеяния окажется равной 0.

 Условие интерференционного максимума равносильно следующим трем уравнениям (уравнения дифракции Лауэ):

.

Обратная решетка.

 Определим значение вектора , который будет удовлетворять условиям дифракции Лауэ. Для этого представим его в виде суммы

 , где h,k,l целые числа, входящие в уравнения Лауэ, а  вектора, подлежащие определению.

Имеем .Это выполняется, если .

 Аналогично имеем для векторов

  

  

 Из этих соотношений следует:

а) вектор  перпендикулярен векторам  и , вектор  перпендикулярен векторам  и , вектор  перпендикулярен векторам и . Это можно записать следующим образом