б) ![]() =2π
=2π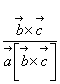 ,
, ![]()
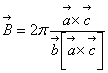 ,
, 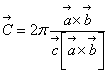 .
В свою очередь
.
В свою очередь
![]() ,
где Ώ объем элементарной ячейки.
,
где Ώ объем элементарной ячейки.
в) ![]() =2π
=2π![]() ,
, ![]()
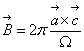 ,
, 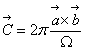 .
.
Определенные таким образом
вектора ![]() ,
, ![]() ,
, ![]() задают новую периодическую
последовательность, так называемую обратную решетку, а сами вектора являются
основными векторами обратной решетки. С их помощью задаются координаты
произвольного узла обратной решетки:
задают новую периодическую
последовательность, так называемую обратную решетку, а сами вектора являются
основными векторами обратной решетки. С их помощью задаются координаты
произвольного узла обратной решетки:
![]() , для которых
выполняются условия дифракции Лауэ.
, для которых
выполняются условия дифракции Лауэ.
Примеры построения обратных решеток.
а) прямая решетка для одномерного случая; обратная решетка
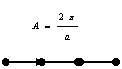
 |
б).
Зонная теория для металлов.
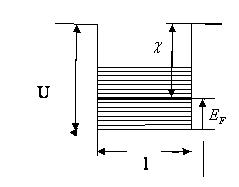 однократно заряженные ионы, образующие потенциальную яму, в ней
практически свободно двигаются электроны. Этот электронный газ компенсирует
силы расталкивания между ионами, в результате образуется прочный кристалл. Этот
вид связи называется металлической связью. На границах кристалла имеется
потенциальный барьер, который не позволяет электронам покидать образец. Все это
отображается в виде следующей энергетической диаграммы. Для расчета
энергетического спектра воспользуемся условием периодичности волновой функции
(условие Борна).
однократно заряженные ионы, образующие потенциальную яму, в ней
практически свободно двигаются электроны. Этот электронный газ компенсирует
силы расталкивания между ионами, в результате образуется прочный кристалл. Этот
вид связи называется металлической связью. На границах кристалла имеется
потенциальный барьер, который не позволяет электронам покидать образец. Все это
отображается в виде следующей энергетической диаграммы. Для расчета
энергетического спектра воспользуемся условием периодичности волновой функции
(условие Борна).![]()
![]()
![]()
![]()
Это справедливо при ![]()
![]() ,
или
,
или ![]() ,
,
Как обычно, ![]()
![]() опять
получаем дискретные
опять
получаем дискретные
значения энергии ![]() .
В случае трехмерной потенциальной ямы волновой вектор
.
В случае трехмерной потенциальной ямы волновой вектор ![]()
![]() , и для энергии
, и для энергии ![]() . Придавая числам
. Придавая числам ![]() значения 0,1,2...,будем получать
различные возможные значения энергии электрона. Введем пространство, где по
осям отложим значения
значения 0,1,2...,будем получать
различные возможные значения энергии электрона. Введем пространство, где по
осям отложим значения
![]() . Каждая точка
соответствует одному энергетическому уровню. Подсчитаем число этих
энергетических уровней, попадающих в сферу радиуса n.
. Каждая точка
соответствует одному энергетическому уровню. Подсчитаем число этих
энергетических уровней, попадающих в сферу радиуса n.
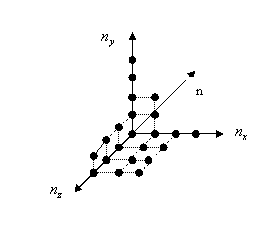
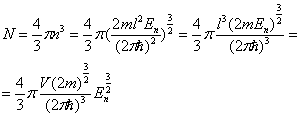
Введем концентрацию уровней ![]()
![]() и сравним ее с концентрацией
электронов. На каждом энергетическом уровне по принципу Паули может
располагаться не более 2-х электронов, причем для металлов известно, что
электроны занимают лишь часть уровней, а часть уровней свободна. Последний
уровень, занятый электронами, определяет энергию Ферми
и сравним ее с концентрацией
электронов. На каждом энергетическом уровне по принципу Паули может
располагаться не более 2-х электронов, причем для металлов известно, что
электроны занимают лишь часть уровней, а часть уровней свободна. Последний
уровень, занятый электронами, определяет энергию Ферми ![]() .
.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.