Квантовая механика, металлы и полупроводники. Волновые свойства частиц (волны де Бройля), страница 18

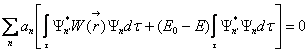
 Введем обозначения: , .

 Интеграл  получил название обменного интеграла, он зависит от степени перекрытия волновых функций и от энергии возмущения . В свою очередь интеграл  определяется только перекрытием волновых функций. С учетом этих обозначений получаем

.

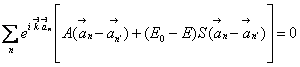 Умножим наше уравнение на постоянный множитель . В результате получим

.

 , где  вектор, соединяющий два узла кристаллической решетки.

 Для энергии электрона в кристалле получаем .

 Последний член определяет добавочную энергию электрона, возникающую за счет взаимодействия с полем кристаллической решетки.

 Для упрощения задачи будем считать, что атомные волновые функции почти не перекрываются. В этом случае =              1 при

                                 0 для всех остальных

 В этом случае , а .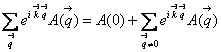

 Обозначим А(0)=С (C<0) и Е=Е₀+С+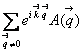

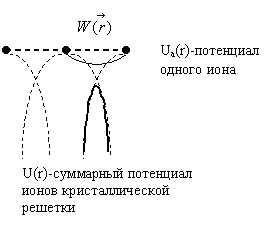
 Здесь необходимо учесть, что  имеет наибольшее значение в области между узлами кристаллической решетки, поэтому, несмотря на малое перекрытие волновых функций,  но только для ближайших соседей. Дальнейшее рассмотрение зависит от состояния электрона в изолированном атоме и от конкретного типа кристаллической решетки.

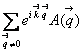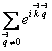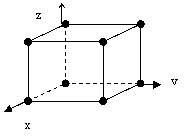
а) Рассмотрим S состояние электрона в изолированном атоме. В этом случае волновая функция обладает сферической симметрией и все ближайшие атомы будут в идентичных условиях(для них  величина постоянная и равна А). =А. Вычислим последнюю сумму для примитивной кубической решетки

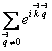=+++++=2{cos(k_xa)+cos(k_ya)+cos(k_za)}

 Для энергии электрона имеем

Е=Е₀+С+2А{cos(k_xa)+cos(k_ya)+cos(k_za)}

 Подведем некоторые итоги нашего рассмотрения

1. Уровень энергии изолированного атома Е₀ за счет взаимодействия с полем решетки смещается на постоянную величину С, знак смещения определяется знаком С.

2. Сам уровень расщепляется в энергетическую зону, внутри которой энергия электрона периодически зависит от компонент волнового вектора .