Квантовая механика, металлы и полупроводники. Волновые свойства частиц (волны де Бройля)

Квантовая механика, металлы и полупроводники.

Волновые свойства частиц (волны де Бройля).

 Рассмотрим 3 постулат Бора:

m v r_n =n                                 (1)

 По предположению де-Бройля частицы обладают волновыми свойствами, на стационарной орбите должно укладываться целое число волн де Бройля:    2πr_n=nλ (2)

 Из уравнений (1) и (2) находим длину волны де Бройля

λ=  =, где р = m v - импульс частицы.

 Оценки показывают, что длина волны имеет разумный размер лишь для микроскопических частиц (электрон, протон, нейтрон ).

 Опытным путем было уставлено полное соответствие длины волны де Бройля с положением максимумов при дифракции электронов на поликристаллической структуре. Опыты Тартаковского-Томсона и Дэвиссона-Джермера.

Волновая функция

 Запишем уравнение плоской волны  Ψ=Ае^{-i (ωt-kx)}.

 Частота ω связана с энергией частицы известным соотношением  E=ω, а волновое число выразим через длину волны де Бройля k=, откуда

Ψ=А exp [-i (]       (3)

 Получена волновая функция для свободной частицы.

Соотношение неопределенностей для волнового числа и координаты волны.

.Как известно, плоская монохроматическая волна (3) занимает все пространство.

Это означает, что, зная точно волновое число к, мы не можем определить положение волны в пространстве. Для уточнения положения волны в пространстве приходится складывать несколько волн с разными значениями волнового вектора к. Этот момент рассмотрим на примере сложения двух волн с волновыми векторами к₁ и к₂:

Ψ₁=Acos (ωt-k₁x) и Ψ₂=Acos (ωt-k₂x)

В заданный момент времени t имеем для суммы двух волн выражение:

Ψ=2Acos (k_ср x) cos[(k₁x –k₂x)/2]= 2Acos [(k₁–k₂)x/2] cos(k_ср x)

 

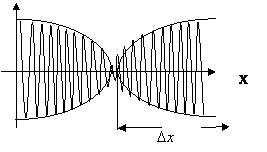С учетом чувствительности прибора, приравняем медленно меняющийся косинус значению ½: ( k₁- k₂)x/2=π/3, 2π/3

х₁=2π/(3 Δk) и х₂=4π/(3 Δk) из этих выражений определим неопределенность координаты Δх =2π/(3 Δk), или Δх Δk

Из этого соотношения видно, что для локализации волнового процесса приходится  увеличивать разброс частот и соответственно Δk.

В применении к волновым свойствам частиц это приводит к следующему:

k=2πp/h , поэтому Δk=Δp/ и Δх Δp. Аналогично для остальных  координат имеем Δх Δp, ΔyΔp, Δz Δp. К этим соотношениям необходимо добавить еще одно соотношение между энергией и временем