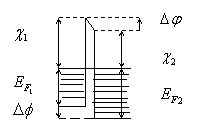Квантовая механика, металлы и полупроводники. Волновые свойства частиц (волны де Бройля), страница 14

При контакте двух металлов на границе раздела образуется тонкий потенциальный барьер практически прозрачный для электронов (ширина его порядка ). Однако электроны из первого металла не могут перейти во второй металл, так как уровни с их энергией заняты. Напротив, электроны из второго металла могут переходить на свободные уровни энергии в первом металле. В результате он будет заряжаться отрицательно, потенциальная энергия электронов будет уменьшатся(энергетические уровни будут смещаться вверх). Второй металл заряжается положительно(энергетические уровни будут смещаться вниз-потенциальная энергия электронов увеличивается). Взаимное перемещение зон будет происходить до тех пор пока не сравняются уровни Ферми обоих металлов. На границе раздела возникает контактная разность потенциалов .

Это внешняя контактная разность потенциалов.

Существует внутренняя контактная разность потенциалов

Если в контакт привести несколько металлов, то разность потенциалов на концах такой цепи будет равна разности потенциалов, определяемой работами выхода крайних образцов металлов. Еще одно следствие: в замкнутой цепи суммарная разность потенциалов равна 0, если все спаи находятся при одинаковой температуре.

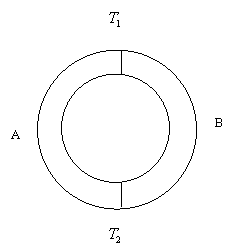Явление Зеебека.

Рассмотрим замкнутую цепь из двух металлов А и В, спаи которых находятся при разных температурах  и . В этом случае в такой замкнутой цепи возникает электрический ток. Можно сказать, что при различных температурах спаев возникает термоэдс. Существует несколько причин возникновения термоэдс.

а) Зависимость уровня Ферми от температуры.

Рассмотрим эту задачу подробнее.

 

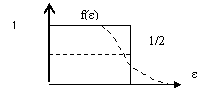Опять воспользуемся постоянством числа электронов:

Для упрощения дальнейших выкладок введем обозначение

Общее количество электронов найдем для температуры Т=0

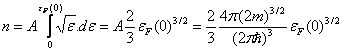. При Т>0 часть электронов перейдет на свободные уровни, лежащие выше уровня Ферми : 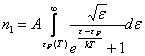, за счет этого часть энергетических уровней ниже уровня Ферми освободятся:

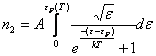
Сохранение числа электронов можно записать таким образом: n(0)=n(T)-n₁+n₂ или

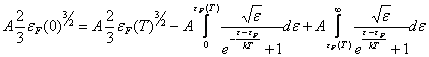
В интегралах произведем замену переменных.

 dε=-kTdx, , пределы ε=0 , ε=ε_F , x=0. Аналогично для второго интеграла: , dε -= dxkT , , и пределы ε=ε_F , x=0, .

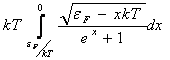
С учетом сделанных замен имеем: ++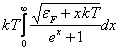= 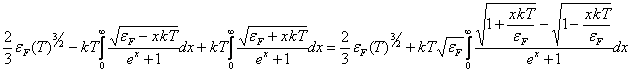     Сучетом малости величины x=kT/ε_F окончательно получим