Метрология, стандартизация, сертификация. Нормирование точности: Лабораторный практикум, страница 9

Чем больше n, тем выше точность оценки параметров теоретического распределения:

;

При n >100 доверительная вероятность того, что , составляет Р = 0,9973.

Таблица 1

Окончание табл. 1

1. Определение точности измерения детали

Обработка результатов измерений

Действительным размером называется размер, получаемый в процессе изготовления или эксплуатации с учетом точности и воспроизводимости измерения.

Результатом технического измерения принято считать величину измерения А с учетом случайной погрешности измерения А± Δ_{изм. сл.} при доверительной вероятности Р.

Систематическая составляющая погрешности измерения предварительно исключается.

Для повышения точности измерений рекомендуется проводить серию измерений в одной точке (не менее трех раз).

Обработка данных измерений:

Полученные отдельные единичные результаты измеряемой величины обозначаются x₁, x₂, x₃,… x_n. Разница между значениями, полученными при измерении объекта, характеризует точность измерения. За действительное значение А измеряемой величины принимается среднее арифметическое  из полученных при измерении отдельных единичных результатов.

Если известно, что систематическая погрешность Δ_{изм. сл.} не изменялась в процессе измерений, то при вычислении результата можно вычислить среднее , а затем исключить из него систематическую погрешность, то есть

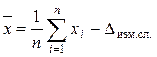
где n – число единичных измерений;  – результат единичного измерения. В противном случае следует исключить систематическую погрешность из каждого измерения U_i , то есть

,

а затем вычислить среднее арифметическое.

Систематическая составляющая погрешности измерения может быть исключена различными методами:

1) Метод введения поправок (предварительная проверка и аттестация мер и измерительных приборов или использование их аттестатов, учет погрешностей шкал, наборов мер и температурных условий).

2) Метод сравнения с образцом.

3) Метод компенсации погрешности по знаку – проведение измерений таким образом, чтобы погрешность вошла в результат измерений с одним знаком, другой раз – с другим.

4) Метод симметричных наблюдений при прогрессивных погрешностях, заключающийся в повторении наблюдений в обратном порядке.

В случае, если , то не исключенными систематическими погрешностями по сравнению со случайными пренебрегают.

Например, при аттестации установлены:

погрешность средства измерения Δ_{ср. изм} = – 0,002 мм,

погрешность измерительного приспособления Δ_∑ = +0,003 мм,

погрешность от условий измерения Δ_усл.и. = + 0,001 мм, остальным можно пренебречь.

Величина суммарной систематической составляющей погрешности измерения равна:

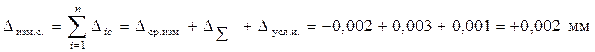
Если часть систематических погрешностей переходит в разряд случайных (например, средство измерения не аттестовано, а известна лишь допустимая погрешность средства измерения  Δ_ic), то их учитывают как случайные, то есть величина суммарной случайной погрешности измерения будет равна:

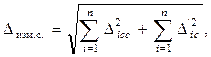
где  – систематические погрешности, перешедшие в разряд случайных.

Доброкачественность измерений определяется отсутствием среди них грубых погрешностей (критерий Греббса-Смирнова). Для исключения из рада грубых погрешностей отбирают единичные измерения с наиболее отклоняющимися от средних значений X_max и X_min и вычисляют отклонение от среднего арифметического: