Метрология, стандартизация, сертификация. Нормирование точности: Лабораторный практикум, страница 8

Случайная погрешность СИ – это составляющая, изменяющаяся при повторных измерениях одной и той же величины случайным образом.

Абсолютная погрешность – разность между показателем СИ (х) и действительным значениемx_д измеряемой величины

∆ = │х – х_д│,

может быть задана:

либо одним числом: ∆ = ±а;

либо в виде линейной зависимости: ∆ = ± вх; ∆ = ±(а ± вх)

 

Рис. 4

Относительная погрешность δ – отношение абсолютной погрешности к действительному х_д значению, выраженное в %:

.

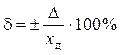Эта формула показывает, что при увеличение х_д; δ стремится к 0, и наоборот, поэтому в метрологии существует запрет измерений на таких участках.

Приведенная погрешность измерений – отношение ∆ к нормируемому значению X_N (в %):

.

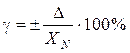Нормирующее значение X_N выбирают в зависимости от вида и характера шкалы прибора.

Различают равномерные и неравномерные шкалы. При равномерной шкале, если «О» на краю, или вне рабочей части шкалы Х_N = X_к, где Х_к – конечное значение; если «О» внутри шкалы – сумме конечных значений шкалы. При неравномерной шкале – длине шкалы.

Для установления пригодности СИ к применению выполняется «поверка» СИ.

Поверка – операция, проводимая уполномоченным органом, заключающаяся в установление пригодности СИ к применению на основании экспериментально определенных метрологических характеристик и контроля их соответствия предъявляемым требованиям.

По результатам поверки выдается свидетельство о поверке, наносится клеймо и т.п.

Поверка проводится методом:

-  непосредственного сравнения измеряемых величин и величин воспроизводимых более точными (образцовыми) мерами или средствами измерений;

-  непосредственного сличения показаний поверяемого прибора и эталона высшего разряда при одновременном измерении одной и той же величины.

Разность этих показаний равняется абсолютной погрешности поверяемого СИ.

Если при поверке вводят поправку на показания «образцовых» приборов (эталонов более высокого порядка), то соотношение погрешностей эталонного и поверяемого СИ составляет 1: 3; если поправки не вводят – 1:5.

Государственная поверочная схема измерений приведена на рис. 4.

3.2.  При изготовлении деталей и их измерениях действует большое число факторов, вызывающих как систематические, так и случайные погрешности изготовления и измерения.

Характеристики точности изготовления и измерений приближенно определяют статистическими методами по результатам опыта.

Для определения точности измерений контроль размеров производят в одной точке несколько раз (не менее трех), не меняя условий замера.

При оценке точности изготовления геометрической формы детали измеряют в нескольких точках (см. табл. 2). Расположение точек должно быть равномерным по длине контролируемого участка детали. При этом за результаты измерений (отклонений) принимаются предельные значения отклонений действительных размеров от номинальных значений

При определении точности изготовления партии деталей измеряют каждую деталь 1-2 раза, причем расположение точки замера должно быть одинаковым (например, у торца валика).

В результате изготовления (измерения) распределение случайных величин подчиняется определенному закону. При нормальном законе распределения его параметрами являются математическое ожидание М(х) = А и среднее квадратичное отклонение σ. Эти параметры приближенно можно оценить но данным измерений (эмпирическому распределению случайных величин):

– среднему арифметическому значению;

S – уточненному среднему квадратичному отклонению (характеризует отклонение единичных наблюдений от)

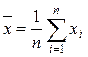  (i = 1, 2, … n)

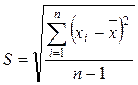
при n > 100 пользуются средним квадратичным отклонением

.

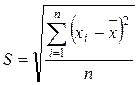Точность оценки результатов измерений, изготовления деталей определяется размерами доверительных интервалов Доверительный интервал это интервал вида , в который с доверительной вероятностью Р попадает теоретическое значение М(х) = А.

,

где t₀ – коэффициент Стьюдента, определяемый по табл. 1;

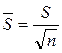  – среднее квадратичное отклонение, характеризующее отклонение  от А (точность измерений)